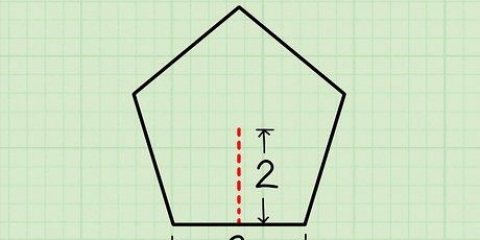
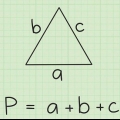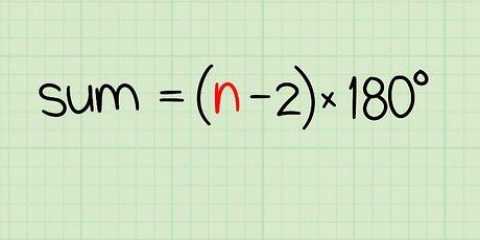Les angles d`un triangle (un polygone à 3 côtés) totalisent 180 degrés. Les angles dans un quadrilatère (un polygone à 4 côtés) totalisent 360 degrés. Les angles d`un pentagone (un polygone à 5 côtés) totalisent 540 degrés. Les angles dans un hexagone (un polygone à 6 côtés) totalisent 720 degrés. Les angles dans un octogone (un polygone à 8 côtés) totalisent 1080 degrés. 
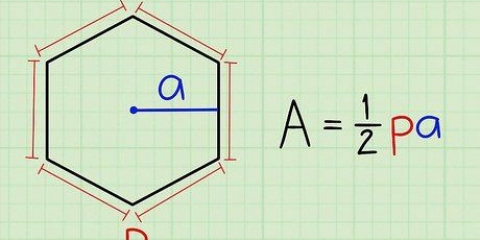
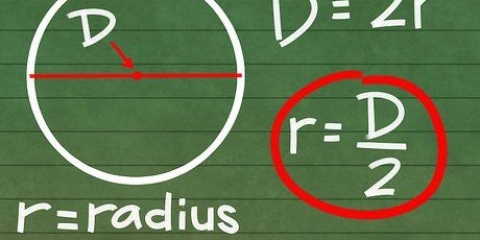
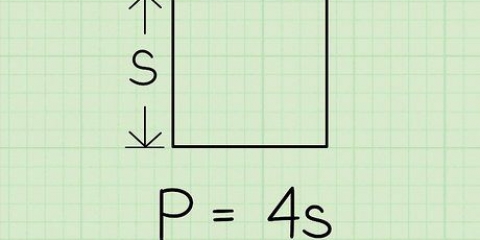
Si le polygone est un polygone régulier, divisez simplement le total de tous les angles par le nombre d`angles. Ainsi, tout angle dans un triangle équilatéral est 180/3=60 degrés, et tout angle d`un carré est 360/4=90 degrés. (Bien que par définition un rectangle ne soit pas un polygone régulier, tous les angles sont aussi des angles droits, et donc 90 degrés). Si un polygone n`est pas un polygone régulier, vous aurez besoin de connaître la magnitude des autres angles pour calculer la magnitude de l`angle inconnu. passer à l`étape suivante. 
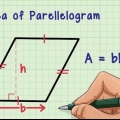
Si deux des angles d`un triangle sont de 60 et 80 degrés, additionnez ces angles ensemble (60 + 80=140). Puis soustraire cette somme du total des angles d`un triangle, 180 degrés : 180-140=40 degrés. (Un tel triangle, où tous les angles sont différents, est appelé un triangle scalène). Vous pouvez écrire la méthode ci-dessus sous forme de formule : une=180 – (b + c), par lequel une est l`angle que vous voulez déterminer, et b et c les angles connus. Pour les polygones avec plus de 3 côtés, remplacez « 180 » par le total des angles spécifiques à ce polygone et ajoutez un terme différent pour chaque angle connu supplémentaire. Pour certains polygones, une "solution plus rapide" est possible pour déterminer l`angle inconnu. Un triangle isocèle est un triangle qui a deux côtés de même longueur et deux angles de même grandeur. Un parallélogramme est un quadrilatère avec des côtés opposés de même longueur et des angles diagonalement opposés de même grandeur. 

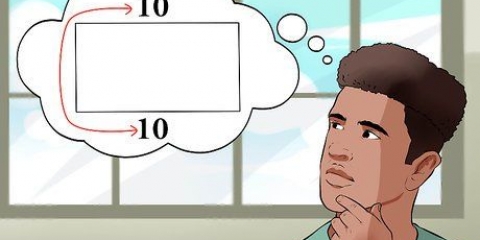
Si vous connaissez la longueur du côté opposé (par rapport à l`angle) et la longueur de l`hypoténuse (le côté opposé à l`angle droit), utilisez la fonction sinus (la longueur du côté opposé divisée par la longueur de l`hypoténuse). soie). Si vous connaissez la longueur du côté rectangulaire adjacent et la longueur de l`hypoténuse, vous pouvez utiliser la fonction cosinus (la longueur du côté adjacent divisée par la longueur de l`hypoténuse). Si vous connaissez les longueurs des côtés opposés et des côtés adjacents, vous pouvez utiliser la fonction tangente (la longueur du côté opposé divisée par la longueur du côté adjacent). 
En divisant la valeur opposée 5 par l`hypoténuse (l`hypoténuse) 10 donne la fraction 5/10=0,5. 
Avant les calculatrices, vous devriez consulter un tableau imprimé de valeurs pour le sinus, le cosinus et la tangente des angles de 0 à 90 degrés. Suivez la colonne sinus jusqu`à ce que vous trouviez la valeur « 0,5 », puis trouvez l`angle qui correspond à cette valeur sinus. Si vous avez une calculatrice avec des fonctions trigonométriques, vous pouvez entrer le sinus comme valeur (si vous n`avez pas déjà utilisé la calculatrice pour diviser le contraire par l`hypoténuse pour trouver cette valeur) puis appuyez sur la ou les touches appropriées. Selon la marque de la calculatrice, appuyez sur une seule touche intitulée « péché » ou sur une touche intitulée « Inv », « 2ndF » ou « Shift » avant d`appuyer sur la touche « péché ». Quelle que soit la méthode que vous utilisez pour résoudre cet exemple, dans tous les cas, vous devriez trouver un angle de 30 degrés.
Calculer des angles
Teneur
En géométrie, un angle est l`espace entre deux rayons ou segments de ligne qui ont la même extrémité ou sommet. La façon la plus courante de mesurer les angles est en degrés, où un cercle complet est de 360 degrés. Vous pouvez calculer l`angle dans un polygone si vous connaissez la forme du polygone et la taille des autres angles ou, dans le cas d`un triangle rectangle, si vous connaissez la taille des deux côtés.
Pas
Méthode 1 sur 2: Calcul de l`angle dans un polygone

1. Compter le nombre de côtés du polygone.

2. Trouver la somme de tous les angles du polygone. La formule pour trouver la mesure totale de tous les angles intérieurs dans un polygone est (m – 2) x 180, où m est le nombre de côtés, ainsi que le nombre d`angles du polygone. Certains totaux courants des angles dans un polygone sont :

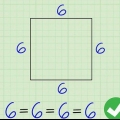
3. Déterminer si le polygone est un polygone régulier. Un polygone régulier est un polygone avec tous les côtés de la même longueur et tous les angles de la même taille. Les triangles et les carrés équilatéraux sont des exemples de polygones réguliers, tandis que le Pentagone à Washington DC est un exemple de pentagone régulier, et un panneau d`arrêt est un exemple d`octogone régulier.

4. Additionnez les angles connus du polygone et soustrayez le total du total de toutes les mesures d`angle du polygone. La plupart des problèmes de géométrie similaires fonctionnent avec des triangles ou des quadrilatères car il y a moins de nombres à traiter, nous allons donc.
Méthode 2 sur 2: Calculer l`angle dans un triangle rectangle

1. Découvrez ce que vous savez déjà. Un triangle rectangle est appelé ainsi parce que l`un de ses angles est un angle droit. Vous pouvez déterminer les autres angles si vous connaissez l`un des éléments suivants :
- La taille du troisième angle. Dans ce cas, vous pouvez ajouter la taille de l`angle à 90, le nombre de degrés de l`angle droit, puis soustraire le total de 180.
- La taille des deux côtés du triangle. Dans ce cas, vous pouvez déterminer l`amplitude de l`angle à l`aide de la trigonométrie.

2. Déterminer quelle fonction trigonométrique utiliser. Les fonctions trigonométriques sont des rapports entre deux des trois côtés d`un triangle. Bien qu`il existe six fonctions trigonométriques, les trois suivantes sont les plus couramment utilisées :

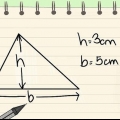
3. Trouver le rapport des deux côtés connus. Pour les besoins de cet exemple, supposons que le côté opposé à l`angle a une longueur de 5 et l`hypoténuse a une longueur de 10. Puisque l`inverse et l`hypoténuse sont ainsi donnés, le rapport dont nous avons affaire ici est celui du sinus.

4. Trouver l`angle correspondant au rapport de la fonction trigonométrique. Puisque nous utilisons le sinus pour trouver l`angle, l`angle que nous recherchons s`appelle l`arc sinus ou sinus inverse. Il y a deux façons de le trouver :
Des astuces
- Les angles sont désignés par le nombre de degrés qu`ils mesurent. Comme mentionné ci-dessus, un angle droit a 90 degrés. Un angle supérieur à 0 mais inférieur à 90 degrés est un angle aigu. Un angle supérieur à 90 mais inférieur à 180 degrés est un angle obtus. Un angle de 180 degrés est un angle droit, tandis qu`un angle supérieur à 180 degrés est un angle rentrant.
- Deux angles avec un total de 90 degrés sont appelés angles complémentaires (Les deux angles autres que l`angle droit dans un triangle rectangle sont des angles complémentaires). Deux angles dont les angles totalisent 180 degrés sont appelés angles supplémentaires.
Nécessités
- Tables trigonométriques ou calculatrice avec fonctions trigonométriques
Articles sur le sujet "Calculer des angles"
Оцените, пожалуйста статью
Populaire