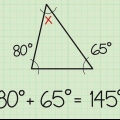
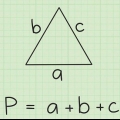a + b > c = 17 > 5 a + c > b = 12 > dix b + c > une = 15 > sept 
5 + 8 > 3 = 13 > 3, donc ce côté est correct. 5 + 3 > 8 = 8 > 8. Parce que ce n`est pas bien, tu peux arrêter maintenant. Ce n`est pas un triangle.
Déterminer si trois longueurs forment ensemble un triangle
Teneur
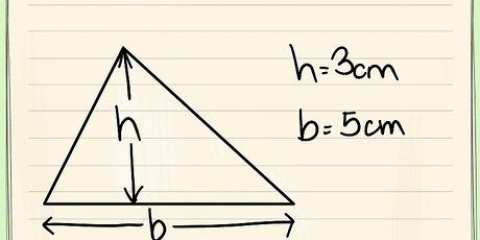
Déterminer si les longueurs de trois côtés forment ensemble un triangle est plus facile qu`il n`y paraît. Tout ce que vous avez à faire est d`utiliser le théorème d`inégalité du triangle, qui stipule que la somme des longueurs des deux côtés d`un triangle est toujours supérieure au troisième côté. Si cela s`applique aux trois combinaisons des longueurs ajoutées, alors vous avez affaire à un triangle.
Pas

1. Apprendre le théorème de l`inégalité triangulaire. Ce théorème stipule que la somme des deux côtés d`un triangle doit être supérieure au troisième côté. Si cela s`applique aux trois combinaisons, alors vous avez un vrai triangle. Vous devrez vérifier ces combinaisons, une par une, pour vous assurer qu`un triangle peut être formé. Vous pouvez également considérer le triangle comme les côtés de longueurs a, b et c, et le théorème comme l`inégalité : a+b > c, a+c > b et b+c > une.
- Un exemple, une = 7, b = 10 et c = 5.

2. Vérifiez si la somme des deux premiers côtés est supérieure au troisième. Dans ce cas, vous pouvez utiliser les côtés une et b additionner, c`est-à-dire 7 + 10, pour obtenir 17, ce qui est supérieur à 5. Vous pouvez également le considérer comme 17 > 5.

3. Vérifiez si la somme de la prochaine combinaison de deux côtés est supérieure au côté restant. Eh bien, il suffit de voir si la somme des côtés une et c est plus grand que le côté b. Cela signifie que vous devez voir si 7 + 5, ou 12, est supérieur à 10. 12 > 10, donc c`est vrai.

4. Vérifiez si la somme de la dernière combinaison de deux côtés est supérieure au côté restant. Vous devrez vérifier si la somme des côtés b et soie c est plus grand que la soie une. Pour ce faire, vous devrez vérifier si 10 + 5 est supérieur à 7. 10 + 5 = 15 et 15 > 7, donc le triangle est correct pour tous les côtés.

5. Vérifie ton travail. Maintenant que vous avez coché tous les côtés un par un, vous pouvez vérifier à nouveau que la règle s`applique aux trois combinaisons. Si la somme de l`un des deux côtés est supérieure au troisième dans n`importe quelle combinaison, comme avec ce triangle, alors vous avez déterminé que le triangle est valide. Si la règle ne s`applique même pas à une seule combinaison, alors ce n`est pas un vrai triangle. Puisque les affirmations suivantes sont vraies, vous avez trouvé un triangle valide :

6. Savoir trouver un triangle invalide. Juste pour comprendre, mais vous devez vous assurer que vous pouvez repérer un triangle qui n`est pas droit. Supposons que vous ayez affaire aux trois côtés et aux longueurs suivants : 5, 8 et 3. Voyons s`ils réussissent le test :
Des astuces
- Cela s`applique toujours, tant que vous ne faites pas d`erreurs de calcul, et si c`est un ajout régulier, c`est très simple.
Articles sur le sujet "Déterminer si trois longueurs forment ensemble un triangle"
Оцените, пожалуйста статью
Similaire
Populaire