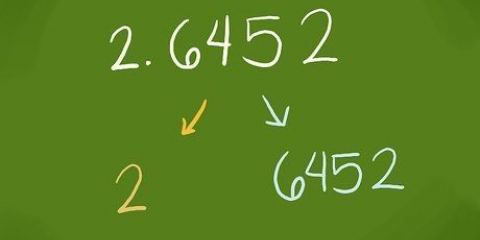Parfois, les nombres de cette rangée auront une virgule décimale, vous cherchez donc en fait 2,5 au lieu de 25. Vous pouvez ignorer ce point décimal car cela n`affectera pas votre réponse. Ignorez également tout point décimal dans le nombre dont vous souhaitez rechercher le logarithme, car la mantisse du log de 1,527 n`est pas différente de celle de 152,7. 














Utilisation de tables logarithmiques
Teneur
Avant l`ère des ordinateurs et des calculatrices, les tables étaient utilisées pour calculer rapidement les logarithmes, les tables de logarithmes. Ces tableaux peuvent toujours être utiles pour calculer ou multiplier rapidement des logarithmes ou de grands nombres, une fois que vous avez compris comment les utiliser.
Pas
Méthode 1 sur 3: Lecture d`une table logarithmique

1. Comprendre ce qu`est un logarithme. 10 vaut 100. 10 vaut 1000. Les puissances 2 et 3 forment des logarithmes avec la base 10, ou encore le log commun de 100 et 1000. En général, a = c être réécrit comme Journalunec = b. Alors "dix à la puissance deux vaut 100" est l`équivalent de "le log de 100 avec la base 10 est deux." Les tables de journal ont une base 10 (utilisez le journal normal), où une donc ça devrait toujours être 10.
- Multiplier deux nombres en additionnant leurs puissances. Par exemple : 10 * 10 = 10, ou 100 * 1000 = 100.000.
- Le logarithme naturel, suggéré par "dans", est le log de base e, où e est la constante 2,718. C`est un nombre utile pour de nombreux domaines des mathématiques et de la physique. Vous pouvez utiliser les tables de logarithme népérien de la même manière que les tables de log classiques, avec la base 10.

2. Déterminez les caractéristiques du nombre dont vous voulez trouver le logarithme népérien. 15 est compris entre 10 (10) et 100 (10), donc son logarithme sera compris entre 1 et 2, si quelque chose comme 1 virgule quelque chose. 150 est compris entre 100 (10) et 1000 (10), donc son logarithme sera compris entre 2 et 3, ou quelque chose comme 2 virgule quelque chose. La virgule quelque chose s`appelle demantisse; c`est ce que vous trouverez dans une table de log. Ce qui est avant la virgule (point décimal) (1 dans le premier exemple, 2 dans le second) est le signifiant.

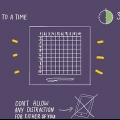
3. Faites glisser votre doigt vers la ligne de droite du tableau, via la colonne à l`extrême gauche. Cette colonne affichera les deux premiers ou, pour certaines grandes tables de journal, les trois chiffres du nombre que vous recherchez le logarithme de. Si vous recherchez le journal de 15,27 dans une table de journal ordinaire, passez à la ligne 15. Si vous recherchez le journal de 2,57, allez à la ligne 25.

4. Dans la bonne ligne, faites glisser votre doigt sur la bonne colonne. Cette colonne est celle marquée par le chiffre suivant du nombre que vous recherchez le logarithme de. Par exemple, si vous voulez trouver le journal de 15.27, votre doigt sera dans la ligne 15. Faites glisser votre doigt le long de la ligne jusqu`à la colonne 2. Vous pointez maintenant vers le nombre 1818. Notez ceci.

5. La table de journal a une table de parties proportionnelles. Faites glisser votre doigt sur la colonne de ce tableau marquée du chiffre suivant du numéro que vous recherchez. Pour 15,27 ce chiffre est 7. Votre doigt est maintenant sur la ligne 15 et la colonne 2. Passez à la ligne 15 et à la colonne des différences moyennes, colonne 7. Vous pointez maintenant vers le nombre 20. Notez ceci.

6. Additionnez les nombres que vous avez trouvés dans les deux étapes précédentes. Pour 15,27 vous obtenez 1838. C`est la mantisse du logarithme de 15,27.

sept. Ajouter le significatif. Puisque 15 est compris entre 10 et 100 (10 et 10), le log de 15 doit être compris entre 1 et 2, donc 1.quelque chose, donc le significatif est 1. Combinez le significatif avec la mantisse pour la réponse finale. Donc le log de 15,27 est 1,1838.
Méthode 2 sur 3: Détermination de l`antilogarithme

1. Comprendre la table antilog. Utilisez ceci lorsque vous avez le journal d`un nombre, mais pas le nombre lui-même. Dans la formule 10 = x, n est le logarithme commun de base 10, ou x. Si vous avez x, vous pouvez trouver n en utilisant la table de journalisation. Si vous connaissez n, déterminez x à l`aide de la table antilog.
- L`antilog est aussi communément appelé log inverse.

2. Notez l`important. C`est le nombre pour la virgule décimale. Si vous voulez rechercher l`antilog de 2.8699, alors le significatif est 2. Dans votre esprit, supprimez ceci du numéro que vous recherchez, mais notez-le pour ne pas l`oublier - cela comptera plus tard.

3. Trouvez la ligne correspondant à la première partie de la mante. en 2.8699, la mantisse est 8699. La plupart des tables antilog, comme la plupart des tables logarithmiques, ont deux nombres dans la colonne la plus à gauche, alors utilisez votre doigt pour suivre la colonne jusqu`à ce que vous arriviez à 86.

4. Faites glisser votre doigt vers la colonne marquée du numéro suivant de la mantisse. Pour 2,8699, faites glisser la ligne marquée 0,86 pour trouver l`intersection avec la colonne 9. Cela devrait vous donner 7396. Notez ceci.

5. Si la table antilog a également une table de parties proportionnelles, faites glisser votre doigt sur la colonne de cette table marquée par le chiffre suivant de la mantisse. Assurez-vous que votre doigt reste dans la même rangée. Dans ce cas, déplacez votre doigt jusqu`à la dernière colonne du tableau, la colonne 9. L`intersection de la ligne 86 et de la colonne 9 avec les différences moyennes est 15. Notez ceci.

6. Additionnez les deux nombres des deux étapes précédentes ensemble. Dans notre exemple, ce sont 7396 et 15. La somme des deux est 7411.

sept. Utilisez le significatif pour placer le point décimal. Le significatif était 2. Cela signifie que la réponse doit être quelque part entre 10 et 10, c`est-à-dire entre 100 et 1000. Pour que le nombre 7411 soit compris entre 100 et 1000, la virgule doit être placée après trois chiffres pour que le nombre soit environ 700, au lieu de 70, ce qui est trop petit, ou 7000, qui est trop grand. La réponse finale est donc 741.1.
Méthode 3 sur 3: Multiplication de nombres à l`aide de tables de journal

1. Comprendre comment multiplier des nombres ensemble en utilisant leurs logarithmes. On sait que 10 * 100 = 1000. Ecrit en puissances (ou logarithmes), cela devient 10 * 10 = 10. On sait aussi que 1 + 2 = 3. De manière générale, 10 * 10 = 10. Donc la somme des logarithmes de deux nombres différents est le logarithme du produit de ces nombres. On peut multiplier deux nombres de même base en additionnant leurs puissances.

2. Recherchez les logarithmes des deux nombres que vous souhaitez multiplier ensemble. Utilisez la méthode ci-dessus pour trouver les logarithmes. Par exemple, si vous voulez multiplier ensemble 15,27 et 48,54, vous constaterez que le log de 15,27 est égal à 1,1838 et le log de 48,54 est 1,6861.

3. Additionnez les deux logarithmes et vous avez trouvé le logarithme de la solution. Dans cet exemple, vous ajoutez 1,1838 et 1,6861 ensemble, et vous obtenez 2,8699. Ce nombre est le logarithme de votre réponse.

4. Recherchez l`antilogarithme du résultat de l`étape supérieure, pour trouver la solution. Pour ce faire, trouvez le nombre dans le tableau le plus proche de la mantisse de ce nombre (8699). Cependant, une méthode plus efficace et fiable consiste à trouver la réponse dans le tableau des antilogarithmes, comme décrit dans la méthode ci-dessus. Dans cet exemple, vous obtenez 741.1.
Des astuces
- Faites toujours les calculs sur une feuille de papier et non par cœur, car ce sont des nombres longs et compliqués, ce qui peut devenir assez délicat.
- Lire attentivement le titre de la page. Un livre de logarithmes a environ 30 pages et si vous utilisez la mauvaise page, votre réponse ne sera plus correcte.
Mises en garde
- Assurez-vous de lire à partir de la même ligne. Parfois, vous pouvez mélanger les lignes et les colonnes en raison des petits nombres et de l`interligne court.
- La plupart des tableaux ne sont précis qu`à 3 ou 4 chiffres. Si vous trouvez l`antilog de 2,8699 avec une calculatrice, la réponse sera arrondie à 741,2, mais la réponse que vous obtenez avec les tables de log est 741.1. Cela est dû à l`arrondissement des tables. Si vous avez besoin d`une réponse plus précise, utilisez une calculatrice ou une autre méthode, plutôt que des tables de logarithmes.
- Utilisez les méthodes décrites dans cet article pour le journal ordinaire, ou logarithme en base 10, et assurez-vous que les nombres que vous recherchez sont également en base 10, également connue sous le nom de notation scientifique.
Nécessités
- table de logarithme ou livre de logarithme
- Papier.
Articles sur le sujet "Utilisation de tables logarithmiques"
Оцените, пожалуйста статью
Populaire