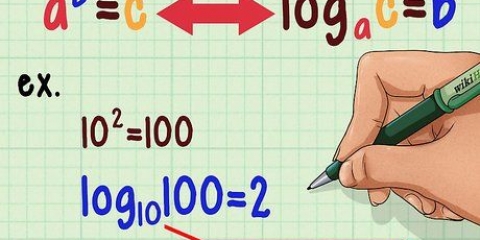
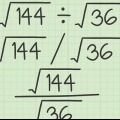Exemple 1 : Résoudre :  .
.
Commencez par convertir cela en logarithme en utilisant la formule ci-dessus : .
. Cette formule est la formule de « changement de base », dérivée des propriétés logarithmiques de base. 
Exemple 1 (suite.): Réécrire  si
si  . La valeur de `?` est la réponse au problème. Vous devrez peut-être en essayer quelques-uns pour le trouver:
. La valeur de `?` est la réponse au problème. Vous devrez peut-être en essayer quelques-uns pour le trouver:



16 est ce que vous cherchiez, alors = 4.
= 4. 
Exemple 2 : Qu`est-ce que  ?
? Convertissez ceci en logarithme : :  .(Notez que le 3 disparaît dans n`importe quel journal initial -- cela s`applique à n`importe quelle base).
.(Notez que le 3 disparaît dans n`importe quel journal initial -- cela s`applique à n`importe quelle base). Réécrire comme  et tester les valeurs possibles de ?:
et tester les valeurs possibles de ?:


Comme 58 se situe entre ces deux nombres, pas d`entier comme réponse.
pas d`entier comme réponse. Laissez votre réponse comme :  .
. 

Si x ou y est négatif, il n`y a pas de solution au problème. si les deux x si y sont négatifs, supprimez les signes négatifs en utilisant la propriété 
Il n`y a pas de logarithmes de nombres négatifs dans l`exemple de problème, vous pouvez donc passer à l`étape suivante. 
Utilisez ceci pour développer le côté gauche de l`exemple de problème :

Remplacez ceci dans l`équation d`origine :

→


L`exemple de problème a un nouveau terme :  . Puisque 3 = 27, simplifiez
. Puisque 3 = 27, simplifiez  méchant 3.
méchant 3. La comparaison complète est maintenant :




 .
.
Dans l`exemple de problème, le m toujours pris dans le terme  .
.
Autour du m pour isoler, utilisez la règle du produit des logarithmes :

Remplacez ceci dans l`équation complète :





Depuis 3 = 19683, n =19683
Partage de logarithmes
Teneur
Les logarithmes peuvent sembler difficiles à utiliser, mais tout comme les exposants ou les polynômes, il vous suffit d`apprendre les bonnes techniques. Il suffit de connaître quelques propriétés de base pour diviser deux logarithmes de même base, ou pour étendre un logarithme par un quotient.
Pas
Méthode 1 sur 2: Division des logarithmes à la main

1. Vérifier les nombres négatifs et ceux. Cette méthode traite des problèmes sous la forme  . Cependant, cela ne fonctionne pas pour quelques cas particuliers :
. Cependant, cela ne fonctionne pas pour quelques cas particuliers :
 . Cependant, cela ne fonctionne pas pour quelques cas particuliers :
. Cependant, cela ne fonctionne pas pour quelques cas particuliers : - Le logarithme d`un nombre négatif n`est pas défini pour toutes les bases (comme
ou
). Ensuite, écrivez `Pas de solution`.
- Le logarithme de zéro est également indéfini pour toutes les bases. Si vous voyez un terme comme
, puis écrivez également `Pas de solution`.
- Le logarithme de un dans n`importe quelle base (
) est toujours égal à zéro, puisque
pour toutes les valeurs de X. Remplacez ce logarithme par 1 au lieu d`utiliser la méthode ci-dessous.
- Si les deux logarithmes ont des bases différentes, comme
, et vous ne pouvez pas simplifier l`un d`eux en un entier, alors le problème ne peut pas être résolu à la main.

2. Modifier l`expression dans un logarithme. En supposant que vous n`ayez trouvé aucune des exceptions ci-dessus, vous pouvez maintenant simplifier le problème en un seul logarithme. Pour ce faire, utilisez la formule .
.
 .
. .
.Commencez par convertir cela en logarithme en utilisant la formule ci-dessus :
 .
.
3. Calculez cela à la main si possible. N`oubliez pas : om  à résoudre, pensez-vous à `
à résoudre, pensez-vous à ` ` ou `Quel exposant puis-je utiliser une élever à X pour obtenir?` Il n`est pas toujours possible de résoudre ce problème sans calculatrice, mais si vous êtes chanceux, vous vous retrouverez avec un logarithme facilement simplifié.
` ou `Quel exposant puis-je utiliser une élever à X pour obtenir?` Il n`est pas toujours possible de résoudre ce problème sans calculatrice, mais si vous êtes chanceux, vous vous retrouverez avec un logarithme facilement simplifié.
 à résoudre, pensez-vous à `
à résoudre, pensez-vous à ` ` ou `Quel exposant puis-je utiliser une élever à X pour obtenir?` Il n`est pas toujours possible de résoudre ce problème sans calculatrice, mais si vous êtes chanceux, vous vous retrouverez avec un logarithme facilement simplifié.
` ou `Quel exposant puis-je utiliser une élever à X pour obtenir?` Il n`est pas toujours possible de résoudre ce problème sans calculatrice, mais si vous êtes chanceux, vous vous retrouverez avec un logarithme facilement simplifié. si
si  . La valeur de `?` est la réponse au problème. Vous devrez peut-être en essayer quelques-uns pour le trouver:
. La valeur de `?` est la réponse au problème. Vous devrez peut-être en essayer quelques-uns pour le trouver:


16 est ce que vous cherchiez, alors
 = 4.
= 4.
4. Laissez la réponse sous forme logarithmique si vous ne pouvez pas la simplifier. Certains logarithmes sont très difficiles à résoudre à la main. Vous avez besoin d`une calculatrice si vous avez besoin de la réponse à des fins pratiques. Lorsque vous résolvez des problèmes en classe de mathématiques, votre professeur s`attend probablement à ce que vous laissiez la réponse sous forme de logarithme. Voici un autre exemple qui utilise cette méthode pour un problème plus délicat :
 ?
? .(Notez que le 3 disparaît dans n`importe quel journal initial -- cela s`applique à n`importe quelle base).
.(Notez que le 3 disparaît dans n`importe quel journal initial -- cela s`applique à n`importe quelle base). et tester les valeurs possibles de ?:
et tester les valeurs possibles de ?:

Comme 58 se situe entre ces deux nombres,
 pas d`entier comme réponse.
pas d`entier comme réponse. .
.Méthode 2 sur 2: Travailler avec le logarithme d`un quotient

1. Commencer par un problème de division dans un logarithme. Cette section vous aide à résoudre des problèmes avec des expressions sous la forme  .
.
 .
. - Par exemple, commencez par ce problème :
`Résoudre pour n si.`

2. Vérifier les nombres négatifs. Le logarithme d`un nombre négatif est indéfini. Si x ou y sont un nombre négatif, vérifiez si le problème a une solution avant de continuer :


3. Diviser le quotient en deux logarithmes. Une propriété utile des logarithmes est décrite par la formule :  . En d`autres termes, le logarithme d`un quotient est toujours égal au logarithme du numérateur, moins le logarithme du dénominateur.
. En d`autres termes, le logarithme d`un quotient est toujours égal au logarithme du numérateur, moins le logarithme du dénominateur.
 . En d`autres termes, le logarithme d`un quotient est toujours égal au logarithme du numérateur, moins le logarithme du dénominateur.
. En d`autres termes, le logarithme d`un quotient est toujours égal au logarithme du numérateur, moins le logarithme du dénominateur.

→


4. Simplifier les logarithmes si possible. Si l`un des nouveaux logarithmes de l`expression est un entier, simplifiez-le maintenant.
 . Puisque 3 = 27, simplifiez
. Puisque 3 = 27, simplifiez  méchant 3.
méchant 3.

5. Isoler la variable. Comme tout problème mathématique, cela aide à isoler le terme avec la variable d`un côté de l`équation. Éliminer les termes similaires lorsque cela est possible pour simplifier l`équation.


 .
.
6. Utiliser des propriétés supplémentaires de logarithmes si nécessaire. Pour isoler la variable des autres termes dans le même logarithme, réécrivez le terme en utilisant différentes propriétés logarithmiques.
 .
.Autour du m pour isoler, utilisez la règle du produit des logarithmes :





sept. Continuez à simplifier jusqu`à ce que vous trouviez la solution. Répétez les mêmes techniques algébriques et logarithmiques pour résoudre le problème. S`il n`y a pas de solution entière, utilisez une calculatrice et arrondir au nombre significatif le plus proche.


Depuis 3 = 19683, n =19683
Articles sur le sujet "Partage de logarithmes"
Оцените, пожалуйста статью
Populaire