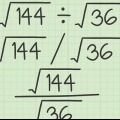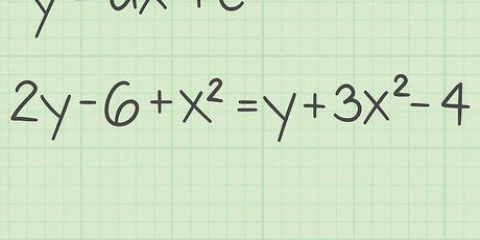Matrices de partage

Teneur

Si vous savez comment multiplier deux matrices entre elles, alors vous êtes sur la bonne voie pour pouvoir "diviser" une matrice par une autre matrice. La division est entre guillemets car les matrices ne peuvent pas techniquement être divisées. Au lieu de cela, nous multiplions la matrice par le inverse d`une autre matrice. Ces calculs sont souvent utilisés pour résoudre des systèmes d`équations linéaires.

Pas

Partie 1 sur 3 : comprendre que le « partage » est impossible

Image intitulée Divide Matrixs Step 1
1. Comprendre ce que signifie « partager » une matrice. Techniquement, la division matricielle n`existe pas. La division des matrices n`est pas une fonction définie. La chose la plus proche est de multiplier par l`inverse d`une autre matrice. En d`autres termes, bien que [A] [B] ne soit pas défini, vous pouvez résoudre le problème [A] * [B]. Étant donné que ces deux équations sont équivalentes à des scalaires, cela "ressemble" à une division matricielle, mais il est important d`utiliser la terminologie correcte.
  • Notez que [A] * [B] et [B] * [A] ne sont pas le même problème. Vous devrez peut-être résoudre les deux pour trouver toutes les réponses possibles.
  • Par exemple, au lieu de (13263913)??(sept423){displaystyle {begin{pmatrix}13&26\39&13end{pmatrix}}div {begin{pmatrix}7&4\2&3end{pmatrix}}}{begin{pmatrix}13&26\39&13end{pmatrix}}div {begin{pmatrix}7&4\2&3end{pmatrix}}, écrivez (13263913)*(sept423)-1{displaystyle {begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}7&4\2&3end{pmatrix}}^{-1}}{begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}7&4\2&3end{pmatrix}}^{{-1}}.
    peut-être que tu devrais aussi (sept423)-1*(13263913){displaystyle {begin{pmatrix}7&4\2&3end{pmatrix}}^{-1}*{begin{pmatrix}13&26\39&13end{pmatrix}}}{begin{pmatrix}7&4\2&3end{pmatrix}}^{{-1}}*{begin{pmatrix}13&26\39&13end{pmatrix}} calculer, ce qui peut donner juste une réponse différente.
Image intitulée Divide Matrixs Step 2
2. Vérifiez que le carré `diviseur-matrice` est. Pour pouvoir déterminer l`inverse d`une matrice, il faut que ce soit une matrice carrée, donc avec le même nombre de lignes et de colonnes. Si la matrice dont vous voulez trouver l`inverse n`est pas une matrice carrée, alors il n`y a pas de solution unique au problème.
  • Le terme "matrice de division" est un peu vague, car il ne s`agit pas vraiment d`un problème de division. Pour [A] * [B], il s`agit de la matrice [B]. Dans notre exemple c`est (sept423){displaystyle {begin{pmatrix}7&4\2&3end{pmatrix}}}{begin{pmatrix}7&4\2&3end{pmatrix}}.
  • Une matrice avec un inverse est dite `inversible` ou `non singulière.`Les matrices sans inverse sont `singulières.`
    • Image intitulée Divide Matrixs Step 3
    3. Vérifiez si les deux matrices peuvent être multipliées ensemble. Pour multiplier deux matrices ensemble, le nombre de colonnes de la première matrice doit être égal au nombre de lignes de la deuxième matrice. Si cela ne fonctionne pas dans les deux cas ([A] * [B] ou [B] * [A]), il n`y a pas de solution au problème.
  • Par exemple, si [A] est une matrice 4 x 3 (4 lignes, 3 colonnes) et [B] est une matrice 2 x 2 (2 lignes, 2 colonnes), alors il n`y a pas de solution. [A] * [B] ne fonctionne pas parce que 3 2, et [B] * [A] ne fonctionne pas parce que 2 4.
  • Sachez que l`inverse [B] a toujours le même nombre de lignes et de colonnes que la matrice d`origine [B]. Il n`est pas nécessaire de calculer l`inverse pour terminer cette étape.
  • Dans notre exemple de problème, les deux matrices sont 2 x 2, elles peuvent donc être multipliées dans n`importe quel ordre.
    • Image intitulée Divide Matrixs Step 4
    4. Déterminer le déterminant d`une matrice 2 x 2. Il y a une vérification supplémentaire avant de pouvoir déterminer l`inverse d`une matrice. Le déterminant de la matrice ne peut pas être nul. Si le déterminant est nul, alors la matrice n`a pas d`inverse. Voici comment déterminer le déterminant dans le cas le plus simple (la matrice 2 x 2) :
  • Matrice 2×2 : le déterminant de la matrice (unebcré){displaystyle {begin{pmatrix}a&avant JC&dend{pmatrix}}}{begin{pmatrix}a&b\c&dend{pmatrix}} est une annonce - bc. En d`autres termes, prenez le produit de la diagonale principale (en haut à gauche en bas à droite), puis en soustrayez le produit de l`antidiagonale (en haut à droite en bas à gauche).
  • Par exemple, la matrice (sept423){displaystyle {begin{pmatrix}7&4\2&3end{pmatrix}}}{begin{pmatrix}7&4\2&3end{pmatrix}} a le déterminant (7)(3) - (4)(2) = 21 - 8 = 13. Ce n`est pas zéro, il est donc possible de déterminer l`inverse.
    • Image intitulée Divide Matrixs Step 5
    5. Déterminer le déterminant d`une matrice plus grande. Si votre matrice est de 3 x 3 ou plus, un travail supplémentaire est nécessaire pour déterminer le déterminant :
  • matrice 3 x 3: Choisissez un élément et traversez la ligne et la colonne auxquelles il appartient. Déterminer le déterminant de la matrice 2 x 2 restante, multiplier par l`élément choisi et conserver un tableau de signe matriciel pour déterminer le signe. Répétez l`opération pour les deux autres éléments de la même ligne et colonne que le premier que vous avez choisi, puis ajoutez les trois déterminants ensemble. Lire cet article pour obtenir des instructions pas à pas et des conseils pour le faire plus rapidement.
  • Matrices plus grandes: L`utilisation d`une calculatrice graphique ou d`un logiciel est recommandée ici. La méthode est similaire à celle d`une matrice 3 x 3, mais prend beaucoup de temps si vous le faites à la main. Par exemple, pour trouver le déterminant d`une matrice 4 x 4, vous devez d`abord trouver les déterminants de quatre matrices 3 x 3.
    • Image intitulée Divide Matrixs Step 6
    6. Continuez. Si votre matrice n`est pas un carré, ou si son déterminant est nul, écrivez-la comme `pas de solution unique`. Le problème est résolu. Si la matrice est un carré et que son déterminant n`est pas nul, passez à la partie suivante pour l`étape suivante : trouver l`inverse.

    Partie 2 sur 3: Inverser la matrice

    Image intitulée Divide Matrixs Step 7
    1. Intervertir les positions des éléments de la diagonale principale 2 x 2. Si vous avez affaire à une matrice 2 x 2, vous pouvez utiliser un raccourci pour rendre ce calcul beaucoup plus facile. La première étape de cette solution rapide consiste à échanger l`élément en haut à gauche avec l`élément en bas à droite. Par exemple:
    • (sept423){displaystyle {begin{pmatrix}7&4\2&3end{pmatrix}}}{begin{pmatrix}7&4\2&3end{pmatrix}} → (342sept){displaystyle {begin{pmatrix}3&4\2&7end{pmatrix}}}{begin{pmatrix}3&4\2&7end{pmatrix}}
    • Remarque: La plupart des gens utilisent une calculatrice pour déterminer l`inverse d`une matrice 3 x 3 (ou plus grande). Si vous souhaitez toujours calculer cela à la main, regardez à la fin de cette partie.
    Image intitulée Divide Matrixs Step 8
    2. Prendre le contraire des deux autres éléments mais les laisser dans cette position. En d`autres termes, multipliez le haut juge et en bas à gauche-éléments avec-1 :
  • (342sept){displaystyle {begin{pmatrix}3&4\2&7end{pmatrix}}}{begin{pmatrix}3&4\2&7end{pmatrix}} → (3-4-2sept){displaystyle {begin{pmatrix}3&-4\-2&7end{pmatrix}}}{begin{pmatrix}3&-4\-2&7end{pmatrix}}
    • Image intitulée Divide Matrixs Step 9
    3. Prenons l`inverse du déterminant. Vous avez trouvé le déterminant de cette matrice dans la section ci-dessus, il n`est donc pas nécessaire de le recalculer. Il suffit d`écrire l`inverse de 1/(déterminant) :
  • Dans notre exemple, le déterminant est 13. La réciproque de ceci est 113{displaystyle {frac {1}{13}}}{frac{1}{13}}.
    • Image intitulée Divide Matrixs Step 10
    4. Multiplier la nouvelle matrice par l`inverse du déterminant. Multipliez chaque élément de la nouvelle matrice par l`inverse que vous venez de trouver. La matrice résultante est l`inverse de la matrice 2 x 2:
  • 113*(3-4-2sept){displaystyle {frac {1}{13}}*{begin{pmatrix}3&-4\-2&7end{pmatrix}}}{frac{1}{13}}*{begin{pmatrix}3&-4\-2&7end{pmatrix}}
    =(313-413-213sept13){displaystyle {begin{pmatrix}{frac {3}{13}}&{frac {-4}{13}}\{frac {-2}{13}}&{frac {7}{13}}end{pmatrix}}}{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}}\{frac{-2}{13}}&{frac{7} {13}}end{pmatrix}}
    • Image intitulée Divide Matrixs Step 11
    5. Confirmez que l`inverse est correct. Pour vérifier votre travail, multipliez l`inverse par la matrice d`origine. Si l`inverse est correct, alors leur produit est toujours l`identité de la matrice, (1001){displaystyle {begin{pmatrix}1&0\0&1end{pmatrix}}}{begin{pmatrix}1&0\0&1end{pmatrix}} Si c`est mathématiquement correct, passez à la section suivante pour terminer l`élaboration du problème.
  • Pour les besoins de l`exemple de problème, nous multiplions (313-413-213sept13)*(sept423)=(1001){displaystyle {begin{pmatrix}{frac {3}{13}}&{frac {-4}{13}}\{frac {-2}{13}}&{frac {7}{13}}end{pmatrix}}*{begin{pmatrix}7&4\2&3end{pmatrix}}={begin{pmatrix}1&0\0&1end{pmatrix}}}{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}}\{frac{-2}{13}}&{frac{7} {13}}end{pmatrix}}*{begin{pmatrix}7&4\2&3end{pmatrix}}={begin{pmatrix}1&0\0&1end{pmatrix} }}.
  • Voir wikihow pour plus d`informations sur la multiplication des matrices.
  • Remarque : La multiplication matricielle n`est pas commutative : l`ordre des facteurs compte. En multipliant une matrice par son inverse, les deux donneront la matrice identité.
    • Image intitulée Divide Matrixs Step 12
    6.Déterminer l`inversion matricielle d`une matrice 3 x 3 ou plus. À moins que vous ne soyez novice dans ce processus, vous pouvez gagner beaucoup de temps en utilisant une calculatrice graphique ou un logiciel de mathématiques sur des matrices plus grandes. Si vous devez le calculer à la main, voici un bref résumé d`une méthode que vous pouvez utiliser :
  • Ajoutez la matrice d`identité I à droite de votre matrice. Par exemple, [B] → [B | JE ]. La matrice d`identité a des éléments `1` le long de la diagonale principale et des éléments `0` dans toutes les autres positions.
  • Effectuez des opérations de ligne pour réduire la matrice jusqu`à ce que le côté gauche soit sous forme d`échelon de ligne, puis continuez à réduire jusqu`à ce que le côté gauche soit la matrice d`identité.
  • Lorsque toute l`opération est terminée, votre matrice est sous la forme [I | B]. En d`autres termes, le côté droit devient l`inverse de la matrice d`origine.

    • Partie 3 sur 3: Multipliez les matrices pour compléter le problème

    Image intitulée Divide Matrixs Step 13
    1. Notez les deux équations possibles. En « mathématiques ordinaires » avec des scalaires, la multiplication est commutative ; 2x6 = 6x2. Cela ne s`applique pas aux matrices, vous devrez donc peut-être résoudre deux problèmes :
    • [A] * [B] est la solution X pour problème X[B] = [A].
    • [B] * [A] est la solution X pour le problème [B]X = [A].
    • Si cela fait partie d`une équation, assurez-vous d`appliquer la même opération aux deux côtés de l`équation. Si [A] = [C], alors [B][A] est ne pas égal à [C][B], car [B] est à gauche de [A], mais à droite de [C].
    Image intitulée Divide Matrixs Step 14
    2. Déterminez les dimensions de votre réponse. Les dimensions de la matrice finale sont les dimensions extérieures des deux facteurs. Il a le même nombre de lignes que la première matrice et le même nombre de colonnes que la deuxième matrice.
  • Revenant à l`exemple initial : les deux (13263913){displaystyle {begin{pmatrix}13&26\39&13end{pmatrix}}}{begin{pmatrix}13&26\39&13end{pmatrix}} et (313-413-213sept13){displaystyle {begin{pmatrix}{frac {3}{13}}&{frac {-4}{13}}\{frac {-2}{13}}&{frac {7}{13}}end{pmatrix}}}{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}}\{frac{-2}{13}}&{frac{7} {13}}end{pmatrix}} sont des matrices de 2 x 2, donc les dimensions de la réponse sont également de 2 x 2.
  • Pour prendre un exemple un peu plus compliqué : si [A] est un 4 x est une matrice 3 et [B] est un 3 x 3 matrice, alors la matrice [A] * [B] a des dimensions 4 x 3.
    • Image intitulée Divide Matrixs Step 15
    3. Déterminer la valeur du premier élément. Consultez l`article lié pour obtenir des instructions détaillées ou actualisez vos connaissances avec ce résumé :
  • Pour trouver la ligne 1, la colonne 1 de [A][B], recherchez le produit scalaire de [A] ligne 1 et [B] colonne 1. Donc, pour une matrice 2 x 2, vous calculez une1,1*b1,1+une1,2*b2,1{displaystyle a_{1,1}*b_{1,1}+a_{1,2}*b_{2,1}}a_{{1,1}}*b_{{1,1}}+a_{{1,2}}*b_{{2,1}}.
  • Dans notre exemple (13263913)*(313-413-213sept13){displaystyle {begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}{frac {3}{13}}&{frac {-4}{13}}\{frac {-2}{13}}&{frac {7}{13}}end{pmatrix}}}{begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}} \{frac{-2}{13}}&{frac{7}{13}}end{pmatrix}}, est la ligne 1 colonne 1 de votre réponse :
    (13*313)+(26*-213){style d`affichage (13*{frac {3}{13}})+(26*{frac {-2}{13}})}(13*{frac{3}{13}})+(26*{frac{-2}{13}})
    =3+-4{style d`affichage =3+-4}=3+-4
    =-1{style d`affichage =-1}=-1
    • Image intitulée Divide Matrixs Step 16
    4. Calculez le produit scalaire pour chaque position dans votre matrice. Par exemple, l`élément à la position 2.1 est le produit scalaire de [A] ligne 2 et [B] colonne 1. Essayez de travailler sur l`exemple vous-même. Vous devriez obtenir les réponses suivantes :
  • (13263913)*(313-413-213sept13)=(-1dixsept-5){displaystyle {begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}{frac {3}{13}}&{frac {-4}{13}}\{frac {-2}{13}}&{frac {7}{13}}end{pmatrix}}={begin{pmatrix}-1&10\7&-5end{pmatrix}}}{begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}} \{frac{-2}{13}}&{frac{7}{13}}end{pmatrix}}={begin{pmatrix}-1&10\7&-5end {pmatrice}}
  • Et l`autre solution : (313-413-213sept13)*(13263913)=(-92193){displaystyle {begin{pmatrix}{frac {3}{13}}&{frac {-4}{13}}\{frac {-2}{13}}&{frac {7}{13}}end{pmatrix}}*{begin{pmatrix}13&26\39&13end{pmatrix}}={begin{pmatrix}-9&2\19&3end{pmatrix}}}{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}}\{frac{-2}{13}}&{frac{7} {13}}end{pmatrix}}*{begin{pmatrix}13&26\39&13end{pmatrix}}={begin{pmatrix}-9&2\19&3end{ pmmatrice}}

    • Des astuces

    • Vous pouvez diviser une matrice par un scalaire, en divisant chaque élément de la matrice par le scalaire.
    • Par exemple, la matrice (6824){displaystyle {begin{pmatrix}6&8\2&4end{pmatrix}}}{begin{pmatrix}6&8\2&4end{pmatrix}} divisé par 2 = (3412){displaystyle {begin{pmatrix}3&4\1&2end{pmatrix}}}{begin{pmatrix}3&4\1&2end{pmatrix}}

    Mises en garde

    • Les calculatrices ne sont pas toujours précises à 100 % en mathématiques matricielles. Par exemple, si votre calculatrice indique qu`un élément a une très petite valeur (par exemple. 2E), alors la valeur est probablement zéro.

    Fr.FaqCartx.info / Éducation et communication
    Оцените, пожалуйста статью
    Nouvelle
    Étirer une toile
    Étirer une toile
    Prenez bien soin de votre peau
    Prenez bien soin de votre peau
    Montrez à un garçon que vous l'aimez
    Montrez à un garçon que vous l'aimez
    Configurer un deuxième compte de messagerie sur yahoo
    Configurer un deuxième compte de messagerie sur yahoo
    Rédiger un plan de traitement en santé mentale
    Rédiger un plan de traitement en santé mentale
    Impression d'un tableau en java
    Impression d'un tableau en java