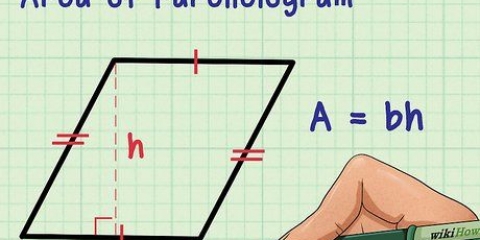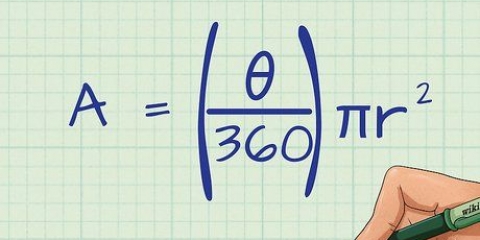La formule pour calculer la longueur de l`apothème est la suivante : la longueur du côté (s) divisé par 2 fois la tangente (tan) de 180 degrés, divisé par le nombre de côtés (m). 

Le périmètre est de 6 x 10 (m X s) est égal à 60 (donc p = 60). L`apothème se calcule en insérant 6 et 10 pour le m et s de la formule. Le résultat de 2tan(180/6) est 1,1547, puis nous divisons 10 par 1,1547 - ce qui équivaut à 8,66. L`aire du polygone est une = une X p / 2 ou 8,66 multiplié par 60 divisé par 2. La solution est une aire de 259,8. Attention, il n`y a pas de parenthèses dans le "surface"-équation, donc 8,66 divisé par 2 multiplié par 60 donne le même résultat, tout comme 60 divisé par 2 multiplié par 8,66. 


Trouver l'aire des polygones réguliers
Teneur
Un polygone régulier est une figure convexe à 2 dimensions avec des côtés congrus et des angles égaux. Pour de nombreux polygones, tels que quadrilatères ou Triangles Il existe des formules simples pour trouver leur aire, mais si vous avez affaire à un polygone, il est probablement préférable de choisir une formule qui utilise l`apothème et le périmètre de la forme. Avec un petit effort, vous pouvez trouver l`aire des polygones réguliers en quelques minutes.
Pas
Partie 1 sur 2: Calcul du périmètre

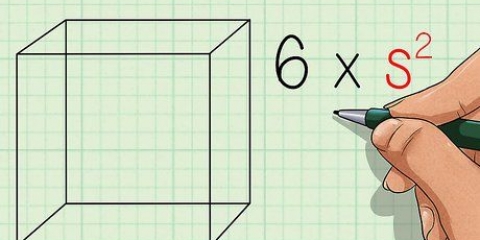
1. Calculer la circonférence. Le périmètre est la longueur combinée du périmètre d`une figure à deux dimensions. Pour un polygone régulier, cela peut être calculé en multipliant la longueur d`un côté par le nombre de côtés (m) de la figure.

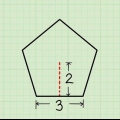
2. Déterminer l`apothème. L`apothème d`un polygone régulier est la distance la plus courte de son centre à chaque côté, créant un angle droit. C`est un peu plus difficile à déterminer que la circonférence.

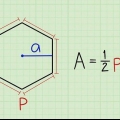
3. Connaître la bonne formule. L`aire d`un polygone régulier est donnée par la formule :Aire = (une X p)/2,par lequel une est la longueur de l`apothème, et p le périmètre du polygone.

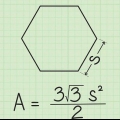
4. Entrez les valeurs deune et p dans la formule pour calculer le périmètre. A titre d`exemple, prenons un hexagone (6 côtés) avec une longueur de 10 pour chaque côté (s).
Partie 2 sur 2: Comprendre les concepts d`une manière différente

1. Un polygone régulier peut être considéré comme une collection de triangles. Chaque côté représente la base d`un triangle, et il y a autant de triangles dans le polygone qu`il y a de côtés. Chacun des triangles est égal en base, en hauteur et en aire.

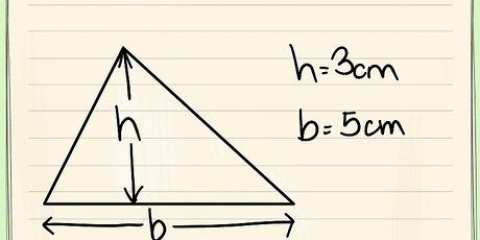
2. Utiliser la formule de l`aire d`un triangle. L`aire d`un triangle est égale à 1/2 de la longueur de sa base (qui est égale à un côté d`un polygone), multipliée par sa hauteur (qui est la même que l`apothème d`un polygone régulier).

3. Remarquez les similitudes. Encore une fois, la formule pour un polygone régulier est 1/2 fois l`apothème multiplié par le périmètre. Le périmètre est la longueur d`un côté multipliée par le nombre de côtés (m); à un polygone régulier représente m aussi le nombre de triangles qui composent la figure. Donc la formule n`est rien de plus que l`aire d`un triangle multipliée par le nombre de triangles dans le polygone.
Des astuces
- Voir wikiHow pour plus d`informations sur l`utilisation racines carrées et racines cubiques.
- Si le dessin de votre octogone (ou de toute forme d`ailleurs) est divisé en triangles et que l`aire d`un triangle est étiquetée, alors vous n`avez plus besoin de l`apothème. Il suffit de prendre l`aire de ce triangle et de la multiplier par le nombre de côtés du polygone d`origine.
Articles sur le sujet "Trouver l'aire des polygones réguliers"
Оцените, пожалуйста статью
Similaire
Populaire