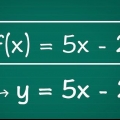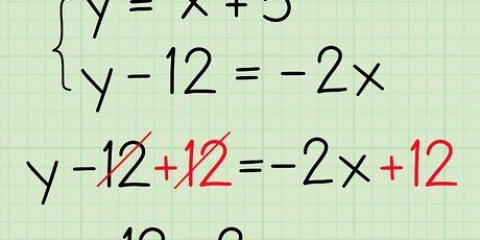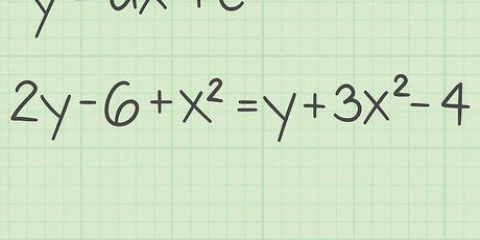devient
devient 
 devient
devient 
 devient
devient  .
.








Si les deux résultats sont les mêmes, alors f(x)=f(-x), et la fonction d`origine est paire. Un exemple est :  et
et  .
.Ces deux sont les mêmes et donc la fonction est même. Si chaque terme de la nouvelle version de la fonction est l`inverse du terme correspondant de l`original, alors f(x)=-f(-x) et la fonction est impaire. Par exemple:  mais
mais  .
.Notez que si vous multipliez chaque terme de la première fonction par -1, vous faites la deuxième fonction. Donc la fonction originale g(x) est impaire. Si la nouvelle fonction ne correspond à aucun de ces deux exemples, alors elle n`est ni paire ni impaire. Par exemple:  mais
mais  . Le premier terme est le même dans toutes les fonctions, mais le deuxième terme est un inverse. Cette fonction n`est donc ni paire ni impaire.
. Le premier terme est le même dans toutes les fonctions, mais le deuxième terme est un inverse. Cette fonction n`est donc ni paire ni impaire.

Vous pouvez tester la symétrie en sélectionnant des points individuels. Si la valeur y de n`importe quelle valeur x est la même que la valeur y de -x, alors la fonction est paire. Les points choisis ci-dessus pour le tracé  donner les résultats suivants :
donner les résultats suivants : (1.3) et (-1.3) (2.9) et (-2.9). Les valeurs y correspondantes pour x=1 et x=-1, et pour x=2 et x=-2, indiquent qu`il s`agit d`une fonction paire. Pour un meilleur test, sélectionner deux points n`est pas une preuve suffisante, mais c`est une bonne indication. 
Si vous choisissez une paire de valeurs de test pour x et leurs valeurs inverses correspondantes pour -x, vous devriez obtenir des résultats inverses. Considérez la fonctionnalité  . Cette fonction renvoie les points suivants :
. Cette fonction renvoie les points suivants :  . Le point est (1,2).
. Le point est (1,2). . Le point est (-1,-2).
. Le point est (-1,-2). . Le point est (2,10).
. Le point est (2,10). . Le point est (-2,-10).
. Le point est (-2,-10).Ainsi f(x)=-f(-x), et vous pouvez conclure que la fonction est impaire. 
Choisissez une paire de valeurs pour x et -x, comme suit :  . Le point à tracer est (1,4).
. Le point à tracer est (1,4). . Le point à tracer est (-1,-2).
. Le point à tracer est (-1,-2). . Le point à tracer est (2,10).
. Le point à tracer est (2,10). . Le point à tracer est (2,-2).
. Le point à tracer est (2,-2).Cela vous donne déjà suffisamment de points pour remarquer qu`il n`y a pas de symétrie. Les valeurs y pour les paires opposées de valeurs x ne sont pas les mêmes, et ne sont pas non plus inverses. Cette fonction n`est ni paire ni impaire. Vous pouvez voir cette fonctionnalité,  , peut être réécrit comme
, peut être réécrit comme  . Écrit sous cette forme, il semble que ce soit une fonction paire car il n`y a qu`un seul exposant, et c`est un nombre pair. Cependant, cet exemple montre que vous ne pouvez pas déterminer si une fonction est paire ou impaire lorsqu`elle est placée entre parenthèses. Vous devez évaluer la fonction en termes individuels, puis examiner les exposants.
. Écrit sous cette forme, il semble que ce soit une fonction paire car il n`y a qu`un seul exposant, et c`est un nombre pair. Cependant, cet exemple montre que vous ne pouvez pas déterminer si une fonction est paire ou impaire lorsqu`elle est placée entre parenthèses. Vous devez évaluer la fonction en termes individuels, puis examiner les exposants.
Savoir si une fonction est paire ou impaire
Teneur
Une façon de classer les fonctions est soit « pair », « impair », ou ni l`un ni l`autre. Ces termes font référence à la répétition ou à la symétrie de la fonction. La meilleure façon de le savoir est de manipuler algébriquement la fonction. Vous pouvez également étudier le graphique de la fonction et rechercher la symétrie. Une fois que vous savez comment classer les caractéristiques, vous pouvez également prédire l`apparition de certaines combinaisons de caractéristiques.
Pas
Méthode 1 sur 2: Test de la fonction algébriquement

1. Afficher les variables inverses. En algèbre, l`inverse d`une variable est négatif. Ceci est vrai ou la variable de la fonction maintenant  est ou autre chose. Si la variable de la fonction d`origine est déjà négative (ou une soustraction), alors sa réciproque est positive (ou une addition). Voici quelques exemples de variables et leurs inverses :
est ou autre chose. Si la variable de la fonction d`origine est déjà négative (ou une soustraction), alors sa réciproque est positive (ou une addition). Voici quelques exemples de variables et leurs inverses :
 est ou autre chose. Si la variable de la fonction d`origine est déjà négative (ou une soustraction), alors sa réciproque est positive (ou une addition). Voici quelques exemples de variables et leurs inverses :
est ou autre chose. Si la variable de la fonction d`origine est déjà négative (ou une soustraction), alors sa réciproque est positive (ou une addition). Voici quelques exemples de variables et leurs inverses : - L`inverse de
est
- L`inverse de
est
- L`inverse de
est
.

2. Remplacer chaque variable de la fonction par son inverse. Ne changez pas la fonction d`origine sauf le caractère. Par exemple:
 devient
devient 
 devient
devient 
 devient
devient  .
.
3. Simplifiez la nouvelle fonctionnalité. À ce stade, vous n`avez pas à vous soucier de résoudre la fonction pour une valeur numérique donnée. Vous simplifiez simplement les variables pour comparer la nouvelle fonction, f(-x), à la fonction d`origine, f(x). Rappelez-vous les règles de base des exposants qui disent qu`une base négative à une puissance paire sera positive, tandis qu`une base négative à une puissance impaire sera négative.








4. Comparez les deux fonctions. Pour chaque exemple que vous essayez, comparez la version simplifiée de f(-x) avec la version originale de f(x). Mettez les termes côte à côte pour une comparaison facile et comparez les signes de tous les termes.
 et
et  .
. mais
mais  .
. mais
mais  . Le premier terme est le même dans toutes les fonctions, mais le deuxième terme est un inverse. Cette fonction n`est donc ni paire ni impaire.
. Le premier terme est le même dans toutes les fonctions, mais le deuxième terme est un inverse. Cette fonction n`est donc ni paire ni impaire.Méthode 2 sur 2: Tester la fonction graphiquement

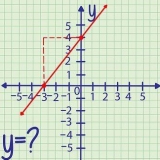
1. Représenter graphiquement la fonction. Utilisez du papier millimétré ou une calculatrice graphique pour représenter graphiquement la fonction. Choisissez différentes valeurs numériques pour  et branchez-le dans la fonction pour obtenir la valeur résultante de
et branchez-le dans la fonction pour obtenir la valeur résultante de  calculer. Tracez ces points sur le graphique et après avoir tracé plusieurs points, tracez une ligne à travers eux pour représenter graphiquement la fonction.
calculer. Tracez ces points sur le graphique et après avoir tracé plusieurs points, tracez une ligne à travers eux pour représenter graphiquement la fonction.
 et branchez-le dans la fonction pour obtenir la valeur résultante de
et branchez-le dans la fonction pour obtenir la valeur résultante de  calculer. Tracez ces points sur le graphique et après avoir tracé plusieurs points, tracez une ligne à travers eux pour représenter graphiquement la fonction.
calculer. Tracez ces points sur le graphique et après avoir tracé plusieurs points, tracez une ligne à travers eux pour représenter graphiquement la fonction. - Lors du tracé des points, faites attention aux valeurs positives et négatives correspondantes pour
. Par exemple, si vous utilisez la fonction
, puis vous tracez les valeurs suivantes :
. Cela se traduit par le point
.
. Cela se traduit par le point
.
. Cela se traduit par le point
.
. Cela se traduit par le point
.

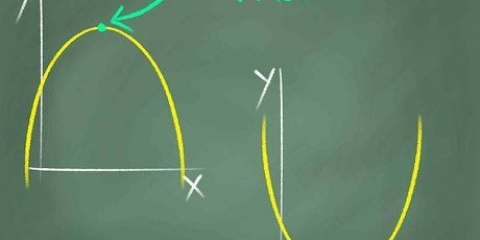
2. Notez la symétrie le long de l`axe des y. En regardant une fonction, la symétrie suggérera une image miroir. Si vous voyez que la partie du graphique du côté droit (positif) de l`axe des y correspond à la partie du graphique du côté gauche (négatif) de l`axe des y, alors le graphique est symétrique par rapport à l`axe des y. Si une fonction est symétrique par rapport à l`axe des y, alors la fonction est paire.
 donner les résultats suivants :
donner les résultats suivants :
3. Test de symétrie depuis l`origine. L`origine est le point central (0,0). La symétrie d`origine signifie qu`un résultat positif pour une valeur x choisie correspondra à un résultat négatif pour -x, et vice versa. Les fonctions impaires présentent une symétrie d`origine.
 . Cette fonction renvoie les points suivants :
. Cette fonction renvoie les points suivants : . Le point est (1,2).
. Le point est (1,2). . Le point est (-1,-2).
. Le point est (-1,-2). . Le point est (2,10).
. Le point est (2,10). . Le point est (-2,-10).
. Le point est (-2,-10).
4. Voir s`il n`y a pas de symétrie. Le dernier exemple est une fonction sans symétrie des deux côtés. Si vous regardez le graphique, vous verrez que ce n`est pas une image miroir ni sur l`axe des y ni autour de l`origine. Voir la fonctionnalité  .
.
 .
. . Le point à tracer est (1,4).
. Le point à tracer est (1,4). . Le point à tracer est (-1,-2).
. Le point à tracer est (-1,-2). . Le point à tracer est (2,10).
. Le point à tracer est (2,10). . Le point à tracer est (2,-2).
. Le point à tracer est (2,-2). , peut être réécrit comme
, peut être réécrit comme  . Écrit sous cette forme, il semble que ce soit une fonction paire car il n`y a qu`un seul exposant, et c`est un nombre pair. Cependant, cet exemple montre que vous ne pouvez pas déterminer si une fonction est paire ou impaire lorsqu`elle est placée entre parenthèses. Vous devez évaluer la fonction en termes individuels, puis examiner les exposants.
. Écrit sous cette forme, il semble que ce soit une fonction paire car il n`y a qu`un seul exposant, et c`est un nombre pair. Cependant, cet exemple montre que vous ne pouvez pas déterminer si une fonction est paire ou impaire lorsqu`elle est placée entre parenthèses. Vous devez évaluer la fonction en termes individuels, puis examiner les exposants.Des astuces
- Si toutes les formes d`une variable dans la fonction ont des exposants pairs, alors la fonction est paire. Si tous les exposants sont impairs, alors la fonction est impaire dans l`ensemble.
Avertissement
- Cet article ne s`applique qu`aux fonctions à deux variables, qui peuvent être représentées graphiquement dans un système de coordonnées à deux dimensions.
Articles sur le sujet "Savoir si une fonction est paire ou impaire"
Оцените, пожалуйста статью
Similaire
Populaire