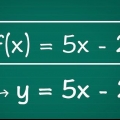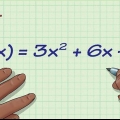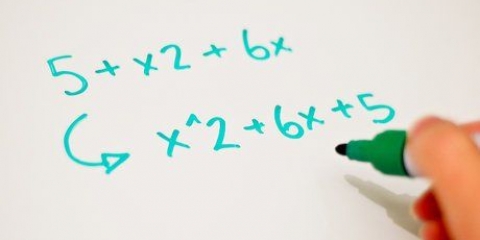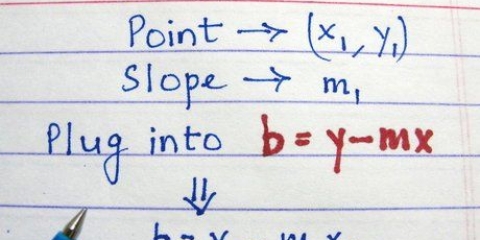Comment représenter graphiquement une fonction : 10 étapes (avec des images)

Teneur

Pas
Des astuces

Comme un graphique voit une équation quadratique hache + bx + c, aussi tout écrit commea(x - h) + k, ressemble à une courbe en U lisse. C`est ce qu`on appelle un parabole. Représenter graphiquement une équation quadratique consiste à trouver le sommet, la direction et souvent les intersections avec l`axe des x et l`axe des y. Dans le cas de l`équation quadratique relativement simple, il peut également suffire d`entrer un certain nombre de valeurs pour x pour indiquer ces points dans le système de coordonnées, après quoi la parabole peut être dessinée. Passez à l`étape 1 pour commencer.

Pas

Image intitulée Tracer une équation quadratique Étape 1

1. Déterminez quel type d`équation quadratique vous avez. Cela peut être écrit de deux manières : la notation standard et la notation de sommet (une autre façon d`écrire la formule de racine carrée). Vous pouvez utiliser les deux pour créer un graphique d`une équation quadratique, mais ce processus est légèrement différent dans les deux cas. Habituellement, vous rencontrerez le formulaire standard, mais cela ne fait certainement pas de mal d`apprendre à utiliser les deux formulaires. Les deux formes d`une équation quadratique sont :

La forme standard. Ici, l`équation quadratique s`écrit : f(x) = ax + bx + c où a, b et c sont des nombres réels et a n`est pas égal à zéro.

Deux exemples d`équations quadratiques standard : f(x) = x + 2x + 1 et f(x) = 9x + 10x -8.

La forme du sommet. Ici, l`équation quadratique s`écrit : f(x) = a(x - h) + k où a, h et k sont des nombres réels et a n`est pas égal à zéro. Cette forme est appelée sommet car h et k se réfèrent directement au sommet de votre parabole au point (h,k).

Deux exemples d`équations sous forme de sommet sont f(x) = 9(x - 4) + 18 et -3(x - 5) + 1

Pour pouvoir faire un graphique de ces équations, nous déterminons d`abord le sommet (h,k) du graphique. Dans l`équation standard, vous pouvez trouver ceci via : h = -b/2a et k = f(h), alors qu`il est déjà donné sous forme de sommet car h et k apparaissent dans l`équation.

Image intitulée Tracer une équation quadratique Étape 2

2. Déterminez vos variables. Pour résoudre une équation quadratique, il est généralement nécessaire de déterminer les variables a, b et c (ou a, h et k). Un problème ordinaire vous donnera une équation quadratique sous la forme standard, mais la notation de sommet peut également se produire.

Par exemple : la fonction standard f(x) = 2x +16x + 39. Ici, nous avons a = 2, b = 16 et c = 39.

En notation de sommet : f(x) = 4(x - 5) + 12. Ici, nous avons a = 4, h = 5 et k = 12.

Image intitulée Tracer une équation quadratique Étape 3

3. Calculer h. Dans la notation de sommet, la valeur de h est déjà donnée, mais dans la notation standard, cette valeur n`a pas encore été calculée. Rappelez-vous que pour l`équation standard, h = -b/2a.

Exemple 1. (f(x) = 2x +16x + 39), h = -b/2a = -16/2(2). En résolvant cela, nous voyons que h = -4.

Exemple 2. (f(x) = 4(x - 5) + 12), on voit tout de suite que h = 5.

Image intitulée Tracer une équation quadratique Étape 4

4. Calculer k. Comme pour h, k est déjà connu pour les équations sous la forme de sommet. Pour les équations en notation standard, rappelez-vous que k = f(h). En d`autres termes, vous pouvez trouver k en remplaçant chaque variable x par la valeur de h.

On a vu par exemple 1 que h = -4. Maintenant, pour trouver k, nous résolvons cette équation en insérant cette valeur de h dans l`équation, pour la variable x :

k = 2(-4) + 16(-4) + 39.

k = 2(16) - 64 + 39.

k = 32 - 64 + 39 = sept

D`après l`exemple 2, nous savons que la valeur de k est égale à 12, sans avoir besoin d`un calcul.

Image intitulée Tracer une équation quadratique Étape 5

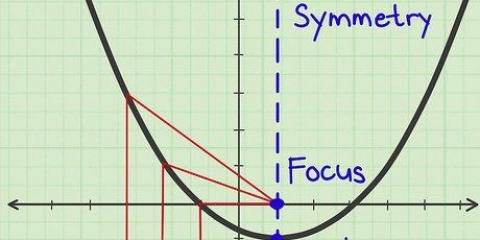
5. Dessiner le haut ou le bas du graphique. La crête ou la vallée de votre parabole est le point (h, k) - h représente la coordonnée x et k représente la coordonnée y. La crête est le centre de votre parabole - le point le plus haut ou le plus bas, la crête ou le creux, d`un graphique sous la forme d`un "VOUS" ou vice versa. Être capable de déterminer le sommet d`une parabole est un élément essentiel pour pouvoir tracer un graphique correct - souvent la détermination du sommet d`une parabole fait partie d`un problème de mathématiques à l`école.

Dans l`exemple 1, le haut du graphique est (-4,7). Dessinez le point sur votre graphique et assurez-vous de nommer les coordonnées correctement.

Dans l`exemple 2, le sommet est (5,12). Donc à partir du point (0,0) vous allez 5 places vers la droite puis 12 vers le haut.

Image intitulée Tracer une équation quadratique Étape 6

6. Tracer l`axe de symétrie de la parabole. L`axe de symétrie d`une parabole est la ligne qui coupe la figure au milieu et la divise exactement en deux. Un côté du graphique est reflété le long de cette ligne dans l`autre côté du graphique. Pour les équations quadratiques de la forme ax + bx + c ou a(x - h) + k, cet axe est la droite parallèle à l`axe y passant par le sommet de la parabole.

Dans le cas de l`exemple 1, l`axe de symétrie est la droite parallèle à l`axe des y et passant par le point (-4, 7). Bien qu`elle ne fasse pas partie de la parabole elle-même, une légère mise en évidence de cette ligne directrice peut vous montrer à quel point la courbe de la parabole est symétrique.

Image intitulée Tracer une équation quadratique Étape 7

sept. Déterminer la direction de la parabole. Après avoir trouvé quel est le sommet de la parabole, il faut savoir s`il s`agit d`une parabole de montagne ou d`une parabole de vallée, c`est-à-dire si l`ouverture est en bas ou en haut. Heureusement c`est très simple. si "une" positif, vous avez affaire à une parabole de vallée ; est "une" négatif alors c`est une parabole de montagne (avec l`ouverture en bas)

Dans l`exemple 1, nous avons affaire à la fonction (f(x) = 2x +16x + 39), et c`est donc une parabole de vallée, car a = 2 (positif).

Dans l`exemple 2, nous avons affaire à la fonction f(x) = 4(x - 5) + 12), et c`est aussi une parabole de vallée car a = 4 (positif).

Image intitulée Tracer une équation quadratique Étape 8

8. Déterminer, si nécessaire, les intersections de la parabole. Souvent, dans les problèmes mathématiques, on vous demande de donner les intersections de la parabole avec l`axe des x (ce sont "nul", une ou deux points où la parabole coupe ou touche l`axe des x). Même s`ils ne sont pas demandés, ces points sont très importants pour pouvoir tracer un graphique précis. Mais toutes les paraboles ne se coupent pas avec l`axe des x. Si vous avez affaire à une parabole de vallée et que le point de la vallée est au-dessus de l`axe des x ou, dans le cas d`une parabole de montagne, juste en dessous de l`axe des x, alors il n`y a tout simplement aucune intersection à trouver. Si tel est le cas, utilisez l`une des méthodes suivantes :

Déterminez que f(x) = 0 et résolvez l`équation. Cette méthode peut fonctionner pour des équations quadratiques simples, en particulier sous la forme de sommet, mais vous constaterez que cela devient de plus en plus difficile à mesure que les fonctions deviennent plus complexes. Ci-dessous quelques exemples.

f(x) = 4(x - 12)

0 = 4(x - 12) - 4

4 = 4(x - 12)

1 = (x - 12)

SqRt(1) = (x - 12)

+/- 1 = x -12. x = 11 et 13 sont les intersections avec l`axe des x de la parabole.

Factoriser l`équation. Certaines équations de la forme ax + bx + c peuvent être facilement réécrites sous la forme (dx + e)(fx +g), où dx × fx = ax, (dx × g + fx × e) = bx, et e × g = c. Dans ce cas, les abscisses sont les valeurs de x où chaque terme entre parenthèses devient 0. Par exemple:

x + 2x + 1

= (x + 1)(x + 1)

Dans ce cas, le point d`intersection est égal à -1 car, une fois rempli avec les deux facteurs, cela donne zéro.

Utiliser la formule abc. S`il n`est pas facile de déterminer les intersections ou de factoriser l`équation, utilisez le "formule abc" qui est spécialement destiné à cette. Supposons une équation sous la forme ax + bx + c. Entrez ensuite les valeurs de a, b et c dans la formule x = (-b +/- SqRt(b - 4ac))/2a. Notez que cela vous donne souvent deux réponses pour x, ce qui est bien - cela signifie simplement que votre parabole a deux intersections avec l`axe des x. Voici un exemple :

-Insérez 5x + 1x + 10 dans l`équation comme suit :

x = (-1 +/- SqRt(1 - 4(-5)(10)))/2(-5)

x = (-1 +/- SqRt(1 + 200))/-10

x = (-1 +/- SqRt(201))/-10

x = (-1 +/- 14,18)/-10

x = (13,18/-10) et (-15,18/-10). Les intersections de la parabole avec l`axe des x sont approximativement x = -1 318 et 1 518

Comme dans l`exemple 1 avec l`équation 2x + 16x + 39, cela ressemblera à ceci :

x = (-16 +/- SqRt (16 - 4(2)(39))))/2(2)

x = (-16 +/- SqRt(256 - 312))/4

x = (-16 +/- SqRt(-56)/-10

Puisqu`il n`est pas possible de trouver la racine carrée d`un nombre négatif, nous savons qu`aucune intersection avec l`axe des x n`existe pour cette parabole particulière.

Image intitulée Représenter graphiquement une équation quadratique Étape 9

9. Si nécessaire, déterminez l`intersection de la parabole avec l`axe des y. Il n`est souvent pas nécessaire, mais parfois nécessaire de trouver ce point d`intersection, par exemple pour un problème de maths. C`est assez simple - définissez la valeur de x sur 0 et résolvez l`équation pour f(x) ou y, ce qui vous donne la valeur y du point où la parabole coupe l`axe des y. La différence avec les intersections par l`axe des x est qu`avec l`axe des y il n`y a toujours qu`un seul point d`intersection. Remarque - pour les équations standard, l`intersection avec l`axe des y est à y = c.

Par exemple, nous savons que notre équation quadratique 2x + 16x + 39 a un point d`intersection y = 39, mais nous pouvons également le trouver comme suit :

f(x) = 2x + 16x + 39

f(x) = 2(0) + 16(0) + 39

f(x) = 39. L`intersection de la parabole avec l`axe des y : y = 39. Comme indiqué ci-dessus, on peut facilement lire l`intersection car y = c.

L`équation 4(x - 5) + 12 a une intersection avec l`axe des y qui peut être trouvée comme suit :

f(x) = 4(x - 5) + 12

f(x) = 4(0 - 5) + 12

f(x) = 4(-5) + 12

f(x) = 4(25) + 12

f(x) = 112. L`intersection avec l`axe des y : y = 112.

Image intitulée Tracer une équation quadratique Étape 10

dix. Si vous trouvez cela nécessaire, dessinez d`abord des points supplémentaires, puis l`ensemble du graphique. Vous devriez maintenant avoir un pic ou une vallée, une direction, des intersections avec l`axe des x et éventuellement avec l`axe des y de votre équation. À partir de ce point, vous pouvez essayer de dessiner la parabole en utilisant ces points ou vous pouvez essayer de trouver plus de points pour rendre le graphique plus précis. La façon la plus simple de le faire est simplement de remplir un certain nombre de valeurs x, ce qui renvoie un certain nombre de valeurs y. Il vous sera souvent demandé (par l`enseignant) de d`abord calculer un nombre de points avant de pouvoir tracer la parabole.

Jetons un autre regard sur l`équation x + 2x + 1. Nous savons déjà que la seule intersection avec l`axe des x est (-1.0). Puisqu`il n`est tangent qu`à l`axe des x en ce point, nous pouvons en déduire que le sommet du graphique est égal à ce point. Jusqu`à présent, nous n`avons qu`un seul point de cette parabole - pas assez pour pouvoir tracer un graphique. Trouvons quelques points supplémentaires pour nous assurer que nous avons plus de valeurs.

Essayons de trouver les valeurs y associées aux valeurs x suivantes : 0, 1, -2 et -3.

x=0 : f(x) = (0) + 2(0) + 1 = 1. Ensuite, le point est (0,1).

x=1 : f(x) = (1) + 2(1) + 1 = 4. Ensuite, le point est (1,4).

x=-2 : f(x) = (-2) + 2(-2) + 1 = 1. Ensuite, le point est (-2.1).

x=-3 : f(x) = (-3) + 2(-3) + 1 = 4. Ensuite, le point est (-3.4).

Placez ces points dans le graphique et tracez votre parabole. Notez que la parabole est complètement symétrique - si vous connaissez les points d`un côté du graphique, vous pouvez généralement vous épargner beaucoup de travail en utilisant ces points pour trouver les points de l`autre côté de l`axe de symétrie.

Des astuces

Arrondissez les nombres si nécessaire ou utilisez des fractions. Cela peut aider à afficher correctement un graphique.
Notez que si, pour la fonction f(x) = ax + bx + c, b ou c sont égaux à zéro, ces termes disparaîtront. Par exemple, 12x + 0x + 6 est égal à 12x + 6 car 0x est égal à 0.