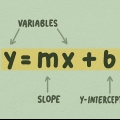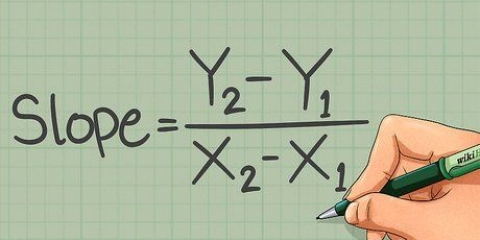Instructions gratuites étape par étape 
Si le coefficient (de pente) une dans l`équation est positive, la parabole s`ouvre vers le haut (dans une parabole orientée verticalement), si la lettre majuscule est `U` et le sommet est un minimum. Comme le une négative, la parabole s`ouvre vers le bas et le sommet a un maximum. Si vous avez du mal à vous en souvenir, pensez-y de cette façon : une équation avec un positif un ressemble à un sourire; une comparaison avec un négatif un ressemble à un froncement de sourcils. Disons que vous avez l`équation suivante : y = 2x -1. Cette parabole a la forme d`un « U » parce que le une (2) est positif. Si l`équation a un terme y au lieu d`un terme x dans la seconde puissance, alors la parabole sera orientée horizontalement et ouverte latéralement (à droite ou à gauche), comme un « C » ou un « C » arrière. Par exemple : la parabole y = x + 3 s`ouvre vers la droite, comme un `C`. 
Dans l`exemple ci-dessus (y = 2x² -1), . est a = 2 et b = 0`.` Vous pouvez maintenant calculer l`axe de symétrie en renseignant les nombres :x = -0 / (2)(2) = 0`.` Dans ce cas, l`axe de symétrie est x = 0 (c`est-à-dire l`axe y du système de coordonnées). 
Les coordonnées du sommet sont aussi appelées (h, k). Dans ce cas h égal à 0 et k égal à -1. L`équation de la parabole peut s`écrire sous la forme y = a(x - h)² + k. Sous cette forme, le sommet est le point (h, k) et vous n`avez besoin de faire aucun calcul pour trouver le sommet autre qu`une interprétation correcte du graphique. 
La valeur médiane de x doit être l`axe de symétrie dans le cas d`une parabole `verticale`. Vous devez inclure au moins deux valeurs au-dessus et en dessous de la valeur médiane de x dans le tableau de symétrie. Dans cet exemple vous placez la valeur de l`axe de symétrie (x = 0) au milieu du tableau. 
si x = -2, alors y: y = (2) (-2) - 1 = 8 - 1 = 7 si x = -1, alors y: y = (2) (-1) - 1 = 2 - 1 = 1 si x = 0, alors y: y = (2) (0) - 1 = 0 - 1 = -1 si x = 1, alors y: y = (2) (1) - 1 = 2 - 1 = 1 si x = 2, alors y: y = (2) (2) - 1 = 8 - 1 = 7 
L`axe des x est horizontal, l`axe des y est vertical. Les nombres positifs sur l`axe des y sont au-dessus et les nombres négatifs en dessous du point (0, 0). Les nombres positifs sur l`axe des x sont à droite et les nombres négatifs à gauche du point (0, 0). 
Dessiner une parabole
Teneur
Une parabole est une courbe bidimensionnelle à symétrie miroir qui a la forme d`un arc. Chaque point de la parabole est équidistant d`un point fixe (le foyer) et d`une droite fixe (la directrice). Pour cartographier une parabole, vous devez trouver le sommet de la parabole, ainsi que certains points de chaque côté, pour marquer le chemin parcouru par les points.
Pas
Partie 1 sur 2: Dessiner une parabole
1. Comprendre les parties d`une parabole. Vous recevrez peut-être des informations avant de commencer, et connaître la terminologie vous aidera à éviter des étapes inutiles. Voici les parties de la parabole que vous devez connaître :
- La mise au point. Un point fixe à l`intérieur de la parabole qui est utilisé pour la définition formelle de la courbe.
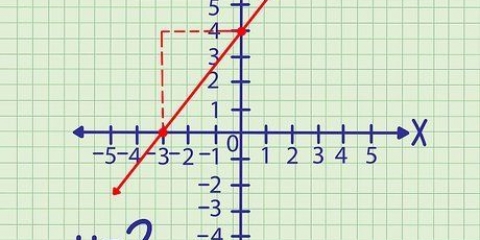
- le réalisateur. Une ligne droite et solide. La parabole est le lieu ou l`ensemble de points dans lequel un point donné est équidistant de la concentrer et le directrice est situé. (Voir tableau ci-dessus.)
- L`axe de symétrie. C`est une droite passant par le sommet de la parabole et équidistante des points correspondants sur les deux bras de la parabole.
- le sommet. Le point où l`axe de symétrie coupe la parabole est appelé le sommet de la parabole. Si la parabole s`ouvre ou vers la droite, le sommet est un le minimum de la courbe. Si la parabole s`ouvre vers le bas ou vers la gauche, le sommet est un maximum.
2. Connaître l`équation d`une parabole. L`équation générale d`une parabole est y = ax+ bx + c. On peut aussi l`écrire sous la forme encore plus générale y = a(x – h)² + k, mais nous nous concentrerons ici sur la première forme de l`équation.
3. Trouver l`axe de symétrie. Rappelez-vous que l`axe de symétrie est la droite qui passe par le point tournant (sommet) de la parabole. Dans le cas d`une parabole verticale (vallée ou montagne), l`axe est le même que la coordonnée x du sommet, c`est-à-dire la valeur x du point où l`axe de symétrie coupe la parabole. Utilisez cette formule pour trouver l`axe de symétrie : x = -b/2a.
4. Trouver le sommet. Une fois que vous connaissez l`axe de symétrie, vous pouvez brancher cette valeur pour x pour obtenir la coordonnée y. Ces deux coordonnées vous donnent le sommet de la parabole. Dans ce cas, vous remplacez 0 par 2x -1 pour obtenir la coordonnée y. y = 2 x 0 -1 = 0 -1 = -1. Le sommet est (0,-1) et la parabole coupe l`axe des y à -1.
5. Créer un tableau de valeurs pour x. Créez un tableau avec certaines valeurs pour x dans la première colonne. Ce tableau vous donne les coordonnées dont vous avez besoin pour représenter graphiquement l`équation.
6. Calculer les valeurs des coordonnées y correspondantes. Remplacez n`importe quelle valeur de x dans l`équation de la parabole et calculez les valeurs correspondantes de y. Mettez ces valeurs calculées de y dans le tableau. Dans cet exemple, les valeurs de y sont calculées comme suit :
sept. Entrez les valeurs calculées de y dans le tableau. Vous avez maintenant trouvé au moins cinq paires de coordonnées pour la parabole et vous êtes presque prêt à dessiner la parabole. Sur la base de votre travail, vous avez maintenant les points suivants : (-2, 7), (-1, 1), (0, -1), (1, 1), (2, 7). Rappelons que la parabole (symétrique) est représentée par rapport à l`axe de symétrie. Cela signifie que les coordonnées y des points directement opposés par rapport à l`axe de symétrie seront égales. Les coordonnées y associées aux coordonnées x -2 et +2 sont toutes les deux 7 ; les coordonnées y appartenant aux coordonnées x -1 et +1 sont toutes les deux 1, et ainsi de suite.
8. Dessiner les points de la table dans le système de coordonnées. Chaque ligne du tableau forme une paire de coordonnées (x, y) sur le système de coordonnées. Dessinez tous les points en utilisant les coordonnées dans le tableau.
9. Relier les points. Pour représenter graphiquement la parabole, reliez les points dessinés à l`étape précédente. Le graphique de cet exemple ressemble à un U. Reliez les points en utilisant des lignes légèrement incurvées (plutôt que droites). Cela crée l`image la plus précise de la parabole (qui est légèrement incurvée sur toute sa longueur). À chaque extrémité de la parabole, vous pouvez dessiner des flèches pointant loin du sommet, si vous le souhaitez. Cela indique que la parabole continue indéfiniment.
Partie 2 sur 2: Déplacement du graphique d`une parabole
Si vous voulez un moyen plus rapide de déplacer une parabole sans avoir à re-trouver son sommet et re-spécifier différents points sur la parabole, alors vous devez comprendre l`équation d`une parabole et apprendre à la convertir verticalement ou horizontalement. Commencez par la parabole de base : y = x. Il a un sommet au point (0, 0) et est une parabole de vallée. Certains points du graphique sont : (-1, 1), (1, 1), (-2, 4) et (2, 4). Vous pouvez déplacer une parabole en fonction de l`équation.
1. Déplacer une parabole vers le haut. Considérez l`équation y = x +1. Cela déplace la parabole d`origine d`une unité. Le sommet est maintenant (0, 1) au lieu de (0, 0). Sa forme n`a pas changé, mais chaque coordonnée y sera décalée d`une unité. Donc au lieu de (-1, 1) et (1, 1), on dessine les points (-1, 2) et (1, 2).
2. Déplacer une parabole vers le bas. Prends l`équation y = x -1. Nous décalons la parabole d`origine d`une unité de sorte que le sommet soit maintenant (0, -1) au lieu de (0, 0,). Elle aura toujours la même forme que la parabole d`origine, mais chaque coordonnée y sera décalée d`une unité. Ainsi, au lieu de (-1, 1) et (1, 1), par exemple, on dessine (-1, 0) et (1, 0).
3. Déplacer une parabole vers la gauche. Considérez l`équation y = (x + 1). Cela décale la parabole d`origine d`une unité vers la gauche. Le sommet est maintenant (-1, 0) au lieu de (0, 0). La forme de la parabole d`origine reste la même, mais chaque coordonnée x est décalée d`un vers la gauche. Par exemple, au lieu de (-1, 1) et (1, 1), on dessine (-2, 1) et (0, 1).
4. Déplacer une parabole vers la droite. Considérez l`équation y = (x - 1). C`est la parabole d`origine décalée d`une unité vers la droite. Le sommet est maintenant (1, 0) au lieu de (0, 0). La forme de la parabole d`origine reste la même, mais chaque coordonnée x est décalée d`une place vers la droite. Par exemple, au lieu de (-1, 1) et (1, 1), on dessine (0, 1) et (2, 1).
Articles sur le sujet "Dessiner une parabole"
Оцените, пожалуйста статью
Similaire
Populaire
