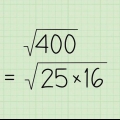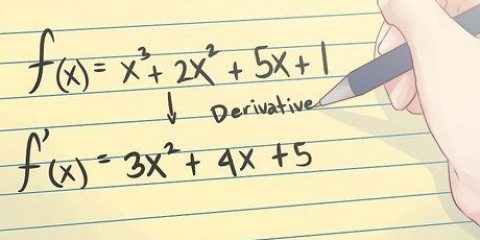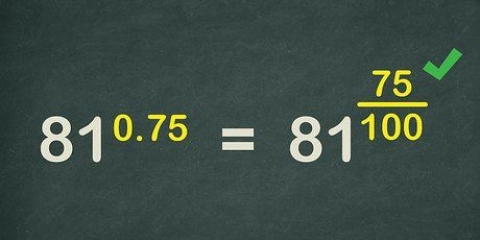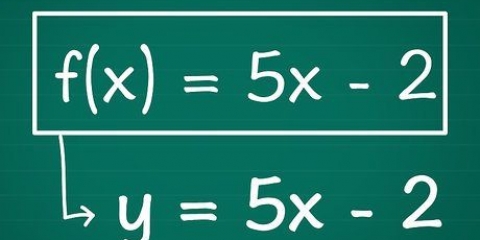Trouver la dérivée de la racine carrée de x

Teneur

Si vous avez suivi des cours de mathématiques à l`école, vous devez avoir appris la règle de puissance pour déterminer la dérivée de fonctions simples. Cependant, lorsque la fonction contient une racine carrée ou un radical, comme $\sqrt{X}$ ${sqrt{x}}$ , alors la règle de puissance semble difficile à appliquer. En utilisant une simple substitution d`exposants, la détermination de la dérivée d`une telle fonction devient très facile. Vous pouvez ensuite appliquer la même substitution et utiliser la règle de la chaîne pour trouver la dérivée de nombreuses autres fonctions avec des racines.

Pas

Méthode 1 sur 3: Appliquer la règle de puissance

Image intitulée Différencier la racine carrée de X Étape 1

1. Revoir la règle de puissance pour les dérivés. La première règle que vous avez probablement apprise pour trouver des dérivés est la règle du pouvoir. Cette règle dit que pour une variable

X

$X$ à la puissance d`un nombre

une

$une$ , est la dérivée et se calcule comme suit :

$F (X) = X une$ ${style d`affichage f(x)=x^{a}}$
$F sexe (X) = une X^{une - 1}$ ${displaystyle f^{prime }(x)=ax^{a-1}}$
Jetez un œil aux exemples de fonctions suivants et à leurs dérivées :

si $F (X) = X 2$ ${style d`affichage f(x)=x^{2}}$ , puis $F sexe (X) = 2 X$ ${displaystyle f^{prime }(x)=2x}$
si $F (X) = 3 X 2$ ${style d`affichage f(x)=3x^{2}}$ , puis $F sexe (X) = 2 * 3 X = 6 X$ ${displaystyle f^{prime }(x)=2*3x=6x}$
si $F (X) = X 3$ ${style d`affichage f(x)=x^{3}}$ , puis $F sexe (X) = 3 X^{2}$ ${displaystyle f^{prime }(x)=3x^{2}}$
si $F (X) = \frac{1}{2} X^{4}$ ${displaystyle f(x)={frac {1}{2}}x^{4}}$ , puis $F sexe (X) = 4 * \frac{1}{2} X^{3} = 2 X^{3}$ ${displaystyle f^{prime }(x)=4*{frac {1}{2}}x^{3}=2x^{3}}$

Image intitulée Différencier la racine carrée de X Étape 2

2. Réécrire la racine carrée en exposant. Pour trouver la dérivée d`une fonction racine carrée, rappelez-vous que la racine carrée d`un nombre ou d`une variable peut également être écrite sous la forme d`un exposant. Le terme sous le radical s`écrit comme une base, et est élevé à la puissance 1/2. Le terme est également utilisé comme exposant de la racine carrée. Examinez les exemples suivants :

\sqrt{X} = X^{\frac{1}{2}}

${displaystyle {sqrt {x}}=x^{frac {1}{2}}}$

\sqrt{4} = 4^{\frac{1}{2}}

${displaystyle {sqrt {4}}=4^{frac {1}{2}}}$

\sqrt{3 X} = (3 X)^{\frac{1}{2}}

${displaystyle {sqrt {3x}}=(3x)^{frac {1}{2}}}$

Image intitulée Différencier la racine carrée de X Étape 3

3. Appliquer la règle du pouvoir. Si la fonction est la racine carrée la plus simple,

F (X) = \sqrt{X}

${displaystyle f(x)={sqrt {x}}}$ , puis appliquez la règle de puissance comme suit pour trouver la dérivée :

F (X) = \sqrt{X}

${displaystyle f(x)={sqrt {x}} }$ (Notez la fonction d`origine.)

F (X) = X (\frac{1}{2})

${displaystyle f(x)=x^{({frac {1}{2}})} }$ (Réécrivez la racine comme un exposant.)

F sexe (X) = \frac{1}{2} X^{(\frac{1}{2} - 1)}

${displaystyle f^{prime }(x)={frac {1}{2}}x^{({frac {1}{2}}-1)} }$ (Trouvez la dérivée en utilisant la règle de puissance.)

F sexe (X) = \frac{1}{2} X^{(- \frac{1}{2})}

${displaystyle f^{prime }(x)={frac {1}{2}}x^{(-{frac {1}{2}})} }$ (Simplifier l`exposant.)

Image intitulée Différencier la racine carrée de X Étape 4

4. Simplifier le résultat. A ce stade, vous devez savoir qu`un exposant négatif signifie que vous prenez l`inverse de ce que serait le nombre avec l`exposant positif. L`exposant de

- \frac{1}{2}

${displaystyle -{frac {1}{2}}}$ signifie que la racine carrée de la base devient le dénominateur d`une fraction.

En continuant avec la racine carrée de la fonction x ci-dessus, la dérivée peut être simplifiée comme suit :

F sexe (X) = \frac{1}{2} X^{- \frac{1}{2}}

${displaystyle f^{prime }(x)={frac {1}{2}}x^{-{frac {1}{2}}}}$

F sexe (X) = \frac{1}{2} * \frac{1}{\sqrt{X}}

${displaystyle f^{prime }(x)={frac {1}{2}}*{frac {1}{sqrt {x}}}}$

F sexe (X) = 12 \sqrt{X}

${displaystyle f^{prime }(x)={frac {1}{2{sqrt {x}}}}}$

Méthode 2 sur 3: Application de la règle de la chaîne pour les fonctions de racine carrée

Image intitulée Différencier la racine carrée de X Étape 5

1. Réviser la règle de chaîne pour les fonctions. La règle de chaîne est une règle pour les dérivés que vous utilisez lorsque la fonction d`origine combine une fonction dans une autre fonction. La règle de la chaîne dit que, pour deux fonctions

F (X)

$f(x)$ et

g (X)

${style d`affichage g(x)}$ , la dérivée de la combinaison des deux fonctions peut être trouvée comme suit :

si $oui = F (g (X))$ ${style d`affichage y=f(g(x))}$ , puis $oui sexe = F^{sexe} (g) * g^{sexe} (X)$ ${displaystyle y^{prime }=f^{prime }(g)*g^{prime }(x)}$ .

Image intitulée Différencier la racine carrée de X Étape 6

2. Définir les fonctions de règle de chaîne. L`utilisation de la règle de la chaîne nécessite que vous définissiez d`abord les deux fonctions qui composent votre fonction combinée. Pour les fonctions racine carrée, la fonction la plus externe est

F (g)

${style d`affichage f(g)}$ la fonction racine carrée et la fonction la plus interne

g (X)

${style d`affichage g(x)}$ la fonction sous le radical.

Par exemple : supposons que vous ayez la dérivée de

\sqrt{3 X + 2}

${style d`affichage {sqrt {3x+2}}}$ veux trouver. Définissez ensuite les deux parties comme suit :

F (g) = \sqrt{g} = g^{\frac{1}{2}}

${displaystyle f(g)={sqrt {g}}=g^{frac {1}{2}}}$

g (X) = (3 X + 2)

${style d`affichage g(x)=(3x+2)}$

Image intitulée Différencier la racine carrée de X Étape 7

3. Trouver les dérivées des deux fonctions. Pour appliquer la règle de la chaîne à la racine carrée d`une fonction, vous devez d`abord trouver la dérivée de la fonction racine carrée générale :

F (g) = \sqrt{g} = g^{\frac{1}{2}}

${displaystyle f(g)={sqrt {g}}=g^{frac {1}{2}}}$

F sexe (g) = \frac{1}{2} g^{- \frac{1}{2}}

${displaystyle f^{prime }(g)={frac {1}{2}}g^{-{frac {1}{2}}}}$

F sexe (g) = 12 \sqrt{g}

${displaystyle f^{prime }(g)={frac {1}{2{sqrt {g}}}}}$

Déterminez ensuite la dérivée de la deuxième fonction :

g (X) = (3 X + 2)

${style d`affichage g(x)=(3x+2)}$

g sexe (X) = 3

${displaystyle g^{prime }(x)=3}$

Image intitulée Différencier la racine carrée de X Étape 8

4. Combiner les fonctions dans la règle de chaîne. La règle de la chaîne est

oui sexe = F^{sexe} (g) * g^{sexe} (X)

${displaystyle y^{prime }=f^{prime }(g)*g^{prime }(x)}$ . Combinez les dérivés comme suit :

oui sexe = 12 \sqrt{g} * 3

${displaystyle y^{prime }={frac {1}{2{sqrt {g}}}}*3}$

oui sexe = 12 \sqrt{(3 X + 2} * 3

${displaystyle y^{prime }={frac {1}{2{sqrt {(3x+2}}}}}*3}$

oui sexe = 32 \sqrt{(3 X + 2}

${displaystyle y^{prime }={frac {3}{2{sqrt {(3x+2}}}}}$

Méthode 3 sur 3: Trouver rapidement les dérivées des fonctions racine

Image intitulée Différencier la racine carrée de X Étape 9

1. Déterminer les dérivées d`une fonction racine carrée à l`aide d`une méthode rapide. Lorsque vous voulez trouver la dérivée de la racine carrée d`une variable ou d`une fonction, vous pouvez appliquer une règle simple : la dérivée sera toujours la dérivée du nombre sous le radical, divisée par le double de la racine carrée d`origine. Symboliquement, cela peut être représenté par :

si $F (X) = \sqrt{vous}$ ${displaystyle f(x)={sqrt {u}}}$ , puis $F sexe (X) = vous sexe 2 \sqrt{vous}$ ${displaystyle f^{prime }(x)={frac {u^{prime }}{2{sqrt {u}}}}}$

Image intitulée Différencier la racine carrée de X Étape 10

2. Trouver la dérivée du nombre sous le radical. Ceci est un nombre ou une fonction sous le signe de la racine carrée. Pour utiliser cette méthode rapide, il suffit de trouver la dérivée du nombre sous le radical. Consultez les exemples suivants :

Dans la fonction

\sqrt{5 X + 2}

${style d`affichage {sqrt {5x+2}}}$ , est le nombre racine

(5 X + 2)

${style d`affichage (5x+2)}$ . La dérivée est

5

$5$ .

Dans la fonction

\sqrt{3 X} 4

${displaystyle {sqrt {3x^{4}}}}$ , est le nombre racine

3 X 4

${displaystyle 3x^{4}}$ . La dérivée est

12 X 3

${displaystyle 12x^{3}}$ .

Dans la fonction

\sqrt{s je m (X)}

${displaystyle {sqrt {sin(x)}}}$ , est le nombre racine

péché ?? (X)

${style d`affichage sin(x)}$ . La dérivée est

car ?? (X)

${style d`affichage cos(x)}$ .

Image intitulée Différencier la racine carrée de X Étape 11

3. Écrire la dérivée de la racine comme numérateur d`une fraction. La dérivée d`une fonction racine carrée contiendra une fraction. Le numérateur de cette fraction est la dérivée de la racine du nombre. Ainsi, dans les exemples de fonctions ci-dessus, la première partie de la dérivée ressemblera à ceci :

F (X) = \sqrt{5 X + 2}

${displaystyle f(x)={sqrt {5x+2}}}$ , puis

F sexe (X) = \frac{5}{dénominateur}

${displaystyle f^{prime }(x)={frac {5}{text{dénominateur}}}}$

F (X) = \sqrt{3 X} 4

${displaystyle f(x)={sqrt {3x^{4}}}}$ , puis

F sexe (X) = 12 X 3 dénominateur

${displaystyle f^{prime }(x)={frac {12x^{3}}{text{dénominateur}}}}$

F (X) = \sqrt{péché ?? (X)}

${displaystyle f(x)={sqrt {sin(x)}}}$ , puis

F sexe (X) = car ?? (X) dénominateur

${displaystyle f^{prime }(x)={frac {cos(x)}{text{dénominateur}}}}$

Image intitulée Différencier la racine carrée de X Étape 12

4. Écrivez le dénominateur comme le double de la racine carrée d`origine. Avec cette méthode rapide, le dénominateur est le double de la fonction racine carrée d`origine. Ainsi, dans les trois exemples de fonctions ci-dessus, les dénominateurs des dérivées sont :

F (X) = \sqrt{5 X + 2}

${displaystyle f(x)={sqrt {5x+2}}}$ , puis

F sexe (X) = compteur 2 \sqrt{5 X + 2}

${displaystyle f^{prime }(x)={frac {text{counter}}{2{sqrt {5x+2}}}}}$

F (X) = \sqrt{3 X} 4

${displaystyle f(x)={sqrt {3x^{4}}}}$ , puis

F sexe (X) = compteur 2 \sqrt{3 X} 4

${displaystyle f^{prime }(x)={frac {text{counter}}{2{sqrt {3x^{4}}}}}}}$

F (X) = \sqrt{péché ?? (X)}

${displaystyle f(x)={sqrt {sin(x)}}}$ , puis

F sexe (X) = compteur 2 \sqrt{péché ?? (X)}

${displaystyle f^{prime }(x)={frac {text{counter}}{2{sqrt {sin(x)}}}}}$

Image intitulée Différencier la racine carrée de X Étape 13

5. Combinez le numérateur et le dénominateur pour trouver la dérivée. Mettez les deux moitiés de la fraction ensemble et le résultat sera la dérivée de la fonction d`origine.