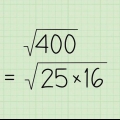Il est clair ici pourquoi  , parce que
, parce que  est au dénominateur et vous ne pouvez pas diviser par zéro.
est au dénominateur et vous ne pouvez pas diviser par zéro. Si vous en avez besoin, vous pouvez étendre le côté gauche pour vous assurer que l`équerrage fonctionne. 

Maintenant, nous pouvons nous débarrasser des signes de valeur absolue, en  placer à droite. Nous pouvons le faire car la valeur absolue ne fait pas la distinction entre les nombres positifs et négatifs, ils sont donc tous les deux valides. Ce détail est pourquoi l`équation quadratique permet d`obtenir deux racines comme résultat.
placer à droite. Nous pouvons le faire car la valeur absolue ne fait pas la distinction entre les nombres positifs et négatifs, ils sont donc tous les deux valides. Ce détail est pourquoi l`équation quadratique permet d`obtenir deux racines comme résultat. 
Simplifions un peu plus cette expression. Puisque la racine carrée d`un quotient est le quotient des racines carrées, nous pouvons écrire le côté droit comme  On peut alors prendre la racine carrée du dénominateur.
On peut alors prendre la racine carrée du dénominateur. 


Apprendre la division carrée
Teneur
L`une des compétences les plus importantes pour les étudiants en mathématiques est la formule abc, ou 


Pas
1. Commencer par la forme standard d`une équation quadratique générale. Bien que toute comparaison avec un terme comme  dans, est quadratique, la forme standard met tout à zéro. Souviens-toi que
dans, est quadratique, la forme standard met tout à zéro. Souviens-toi que  sont des coefficients qui peuvent être n`importe quel entier, donc maintenant vous ne pouvez pas remplir de nombres pour les variables - nous voulons travailler avec la forme générale.
sont des coefficients qui peuvent être n`importe quel entier, donc maintenant vous ne pouvez pas remplir de nombres pour les variables - nous voulons travailler avec la forme générale.
 dans, est quadratique, la forme standard met tout à zéro. Souviens-toi que
dans, est quadratique, la forme standard met tout à zéro. Souviens-toi que  sont des coefficients qui peuvent être n`importe quel entier, donc maintenant vous ne pouvez pas remplir de nombres pour les variables - nous voulons travailler avec la forme générale.
sont des coefficients qui peuvent être n`importe quel entier, donc maintenant vous ne pouvez pas remplir de nombres pour les variables - nous voulons travailler avec la forme générale. - La seule condition est que
, sinon l`équation est simplifiée en une équation linéaire. Voyez si vous pouvez trouver des solutions générales pour des cas particuliers où
et
.
2. tirer c  hors des deux côtés. Notre objectif est d`isoler
hors des deux côtés. Notre objectif est d`isoler  . Nous commençons par déplacer l`un des coefficients de l`autre côté de sorte que le côté gauche ne soit constitué que de termes avec
. Nous commençons par déplacer l`un des coefficients de l`autre côté de sorte que le côté gauche ne soit constitué que de termes avec  .
.
 hors des deux côtés. Notre objectif est d`isoler
hors des deux côtés. Notre objectif est d`isoler  . Nous commençons par déplacer l`un des coefficients de l`autre côté de sorte que le côté gauche ne soit constitué que de termes avec
. Nous commençons par déplacer l`un des coefficients de l`autre côté de sorte que le côté gauche ne soit constitué que de termes avec  .
.
3. Diviser les deux côtés une  . Notez que nous aurions pu les échanger à l`étape précédente et obtenir toujours la même réponse. Rappelez-vous que diviser un polynôme par quelque chose implique de diviser chacun de ses termes individuels. Cela facilite la division du carré.
. Notez que nous aurions pu les échanger à l`étape précédente et obtenir toujours la même réponse. Rappelez-vous que diviser un polynôme par quelque chose implique de diviser chacun de ses termes individuels. Cela facilite la division du carré.
 . Notez que nous aurions pu les échanger à l`étape précédente et obtenir toujours la même réponse. Rappelez-vous que diviser un polynôme par quelque chose implique de diviser chacun de ses termes individuels. Cela facilite la division du carré.
. Notez que nous aurions pu les échanger à l`étape précédente et obtenir toujours la même réponse. Rappelez-vous que diviser un polynôme par quelque chose implique de diviser chacun de ses termes individuels. Cela facilite la division du carré.
4.Diviser le carré. Rappelez-vous que le but est de créer une expression  réécrire comme
réécrire comme  par lequel
par lequel  est un coefficient. Cela peut ne pas être immédiatement clair pour vous. Pour que ce soit plus clair, réécrivez
est un coefficient. Cela peut ne pas être immédiatement clair pour vous. Pour que ce soit plus clair, réécrivez  si
si  en multipliant le terme par
en multipliant le terme par  Nous pouvons le faire car multiplier par 1 ne change rien. Nous pouvons maintenant voir clairement dans notre cas que
Nous pouvons le faire car multiplier par 1 ne change rien. Nous pouvons maintenant voir clairement dans notre cas que  , donc il ne manque que le terme
, donc il ne manque que le terme  . Ainsi, afin de diviser le carré, nous l`ajoutons des deux côtés - à savoir,
. Ainsi, afin de diviser le carré, nous l`ajoutons des deux côtés - à savoir,  Et puis bien sûr on peut factoriser.
Et puis bien sûr on peut factoriser.
 réécrire comme
réécrire comme  par lequel
par lequel  est un coefficient. Cela peut ne pas être immédiatement clair pour vous. Pour que ce soit plus clair, réécrivez
est un coefficient. Cela peut ne pas être immédiatement clair pour vous. Pour que ce soit plus clair, réécrivez  si
si  en multipliant le terme par
en multipliant le terme par  Nous pouvons le faire car multiplier par 1 ne change rien. Nous pouvons maintenant voir clairement dans notre cas que
Nous pouvons le faire car multiplier par 1 ne change rien. Nous pouvons maintenant voir clairement dans notre cas que  , donc il ne manque que le terme
, donc il ne manque que le terme  . Ainsi, afin de diviser le carré, nous l`ajoutons des deux côtés - à savoir,
. Ainsi, afin de diviser le carré, nous l`ajoutons des deux côtés - à savoir,  Et puis bien sûr on peut factoriser.
Et puis bien sûr on peut factoriser.
 , parce que
, parce que  est au dénominateur et vous ne pouvez pas diviser par zéro.
est au dénominateur et vous ne pouvez pas diviser par zéro.5. Écrivez le côté droit sous un dénominateur commun. Nous voulons que les deux dénominateurs soient  sont, alors multipliez le terme
sont, alors multipliez le terme  de
de  .
.
 sont, alors multipliez le terme
sont, alors multipliez le terme  de
de  .
.
6. Calculer la racine carrée des deux côtés. Cependant, il est essentiel que vous compreniez qu`en faisant cela, vous suivez essentiellement deux étapes. Lorsque vous prenez la racine carrée de  , alors vous obtenez
, alors vous obtenez  ne pas. Vous obtenez essentiellement la valeur absolue de celui-ci,
ne pas. Vous obtenez essentiellement la valeur absolue de celui-ci,  . Cette valeur absolue est essentiel pour obtenir les deux racines - le simple fait de placer des racines carrées au-dessus des deux côtés ne donnera qu`une seule des racines.
. Cette valeur absolue est essentiel pour obtenir les deux racines - le simple fait de placer des racines carrées au-dessus des deux côtés ne donnera qu`une seule des racines.
 , alors vous obtenez
, alors vous obtenez  ne pas. Vous obtenez essentiellement la valeur absolue de celui-ci,
ne pas. Vous obtenez essentiellement la valeur absolue de celui-ci,  . Cette valeur absolue est essentiel pour obtenir les deux racines - le simple fait de placer des racines carrées au-dessus des deux côtés ne donnera qu`une seule des racines.
. Cette valeur absolue est essentiel pour obtenir les deux racines - le simple fait de placer des racines carrées au-dessus des deux côtés ne donnera qu`une seule des racines.
 placer à droite. Nous pouvons le faire car la valeur absolue ne fait pas la distinction entre les nombres positifs et négatifs, ils sont donc tous les deux valides. Ce détail est pourquoi l`équation quadratique permet d`obtenir deux racines comme résultat.
placer à droite. Nous pouvons le faire car la valeur absolue ne fait pas la distinction entre les nombres positifs et négatifs, ils sont donc tous les deux valides. Ce détail est pourquoi l`équation quadratique permet d`obtenir deux racines comme résultat.
 On peut alors prendre la racine carrée du dénominateur.
On peut alors prendre la racine carrée du dénominateur.
sept. isoler X  en soustrayant
en soustrayant b 2 une  sur les deux côtés.
sur les deux côtés.
 en soustrayant
en soustrayant  sur les deux côtés.
sur les deux côtés.
8. Écrivez le côté droit sous un dénominateur commun. Ce n`est pas comme la formule abc, la formule pour résoudre une équation quadratique sous forme standard. Cela fonctionne pour n`importe quel  et donne
et donne  par conséquent, qui peut être un nombre réel ou complexe. Pour vérifier que ce processus fonctionne, suivez simplement les étapes de cet article dans l`ordre inverse pour revenir au formulaire par défaut.
par conséquent, qui peut être un nombre réel ou complexe. Pour vérifier que ce processus fonctionne, suivez simplement les étapes de cet article dans l`ordre inverse pour revenir au formulaire par défaut.
 et donne
et donne  par conséquent, qui peut être un nombre réel ou complexe. Pour vérifier que ce processus fonctionne, suivez simplement les étapes de cet article dans l`ordre inverse pour revenir au formulaire par défaut.
par conséquent, qui peut être un nombre réel ou complexe. Pour vérifier que ce processus fonctionne, suivez simplement les étapes de cet article dans l`ordre inverse pour revenir au formulaire par défaut.
Des astuces
- Il est intéressant de noter que la formule abc s`applique également aux coefficients complexes, bien qu`il faille simplifier un peu plus pour obtenir la réponse finale, et les racines ne sont pas des paires conjuguées. Les problèmes avec les expressions quadratiques sont, cependant, presque toujours donnés avec des coefficients réels.
Articles sur le sujet "Apprendre la division carrée"
Оцените, пожалуйста статью
Similaire
Populaire