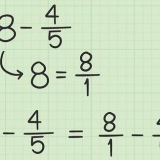heinchauves-souris mlever huit Wtic Vmultiplier réelen ôcompter unesoustraire L`ordre des opérations est important en mathématiques, car un mauvais ordre peut entraîner la recherche d`une réponse différente. Par exemple, si vous avez le problème 8 + 2 × 5, et que vous ajoutez d`abord 2 à 8, vous obtenez 10 × 5 =50 comme réponse. Mais si vous multipliez d`abord 2 par 5, il s`ensuit que 8 + 10=18. Seule la deuxième réponse est correcte. 
Sur une droite numérique, une version négative d`un nombre est aussi loin de zéro que du côté positif, mais dans la direction opposée. L`addition de deux nombres négatifs fait la somme plus négatif (en d`autres termes, les nombres grossissent, mais comme le nombre est négatif, c`est un nombre inférieur). Deux signes négatifs s`annulent - soustraire un nombre négatif revient à ajouter un nombre positif. Multiplier ou diviser deux nombres négatifs donne une réponse positive. Multiplier ou diviser un nombre positif et un nombre négatif donne une réponse négative. 
Par exemple, pour résoudre l`équation 9/3 - 5 + 3 × 4, nous arrangerions notre problème comme ceci : 

Par exemple, dans l`équation 2x + 3=11, x est la variable. Cela signifie qu`il y a une valeur qui peut être substituée au x pour rendre le côté gauche de l`équation égal à 11. Puisque 2 × 4 + 3=11, dans ce cas x=4. Un moyen simple de comprendre les variables est de les remplacer par un point d`interrogation dans les problèmes d`algèbre. Par exemple : réécrivez l`équation 2 + 3 + x=9 comme 2 + 3 + ?=9. Cela permet de voir facilement quel est le point - nous devons déterminer quel nombre ajouter à 2 + 3 = 5 pour obtenir 9 comme réponse. La réponse est encore 4, Bien sûr. 
Par exemple : regardez l`équation 2x + 1x=9. Dans ce cas, nous ajoutons 2x et 1x ensemble pour obtenir 3x=9. Puisque 3 x 3=9, nous savons maintenant que x=3. Notez encore une fois que vous ne pouvez ajouter que des variables qui sont égales. Dans l`équation 2x + 1y=9, on ne peut pas combiner 2x et 1y car ce sont deux variables différentes. Ceci est également vrai lorsqu`une variable a un exposant différent de l`autre. Par exemple, dans l`équation 2x + 3x=10, 2x et 3x ne peuvent pas être combinés car les variables x ont des exposants différents. Pour plus d`informations sur l`ajout d`exposants, voir wikiHow. 

En général, l`addition et la soustraction sont « opposées » — on fonctionne comme. Voir ci-dessous: 
Avec la multiplication et la division, vous devez effectuer l`opération inverse sur tout de l`autre côté du signe égal, même s`il s`agit de plusieurs nombres. Voir ci-dessous: 
Cela peut être un peu déroutant, mais dans ces cas, vous prenez la racine carrée des deux côtés lorsque vous avez affaire à un exposant. D`autre part, vous prenez également l`exposant des deux côtés lorsque vous avez affaire à une racine carrée. Voir ci-dessous: 

Par exemple : supposons que nous ayons un terrain de football qui mesure 30 mètres de plus que large. Nous utilisons l`équation l=w + 30 pour représenter ce. Nous pouvons tester cette équation en entrant des valeurs simples pour w. Par exemple, si le champ mesure w=10 mètres de large, alors il fera 10 + 30=40 mètres de long. S`il fait 30 mètres de large, alors ce sera 30 + 30 = 60 mètres de long, etc. Cela semble logique - nous nous attendons à ce que le champ s`allonge à mesure qu`il s`élargit, donc cette équation semble être une solution raisonnable. 
Par exemple, supposons que nous réduisions une équation algébrique à x=1250. Si nous entrons 1250 dans une calculatrice, nous obtenons une énorme série de décimales (parce que l`écran de la calculatrice a un espace limité, il ne peut pas afficher la réponse complète). Dans ce cas, nous pouvons simplement afficher la réponse sous la forme 1250 ou simplifier la réponse en l`écrivant en notation scientifique. 
Factoriser les équations de la forme ax + ba en a(x + b). Exemple : 2x + 4=2(x + 2) Équations de factorisation de la forme ax + bx à cx((a/c)x + (b/c)) où c est le plus grand nombre dans lequel a et b s`intègrent complètement. Exemple : 3y + 12y=3y(y + 4) Les équations de la forme x + bx + c se transforment en (x + y)(x + z) où y × z=c et yx + zx=bx. Exemple : x + 4x + 3=(x + 3)(x + 1). 

Si, pour une raison quelconque, votre professeur ne peut pas vous aider, demandez-lui quelles sont les options de tutorat à l`école. De nombreuses écoles ont des cours supplémentaires qui vous donnent le temps et l`attention supplémentaires dont vous avez besoin pour exceller en algèbre. N`oubliez pas qu`il n`y a pas de honte à profiter de l`aide gratuite disponible - c`est une indication que vous êtes assez intelligent pour résoudre vos problèmes! 

Par exemple, dans l`équation 3 > 5x - 2, nous résolvons cela de la même manière qu`une équation normale : Cela implique que tout nombre inférieur à 1 est correct pour x. En d`autres termes, x peut être 0, -1, -2 etc. sont. Si nous insérons ces nombres dans l`équation pour x, nous obtenons toujours une réponse inférieure à 3. 
Un exemple : résolution de la formule quadratique 3x + 2x -1=0. 
Par exemple : supposons que nous ayons affaire à un système d`équations y=3x - 2 et y=-x - 6. Si nous traçons ces deux lignes sur un graphique, nous obtenons une ligne qui monte fortement et une qui descend moins fortement. Parce que ces lignes se coupent au point (-1,-5), est que la solution du système. Si vous voulez vérifier cela, traitez la réponse dans les équations du système - une bonne réponse devrait « fonctionner » pour les deux équations. Les deux équations sont « correctes », donc notre réponse est correcte!
Apprendre l'algèbre
Teneur
L`apprentissage de l`algèbre est important pour progresser dans presque toutes les parties des mathématiques dans l`enseignement secondaire et supérieur. Chaque niveau de mathématiques est construit sur la base, et avec cela, chaque niveau de mathématiques est particulièrement important. Cependant, même les compétences mathématiques les plus élémentaires peuvent être difficiles à saisir pour les débutants lorsqu`ils sont confrontés pour la première fois. Si vous êtes aux prises avec des sujets fondamentaux de l`algèbre, ne vous inquiétez pas. Avec une petite explication, quelques exemples simples et quelques conseils pour améliorer vos compétences, vous serez bientôt un maître en algèbre.
Pas
Partie 1 sur 5: Apprendre les règles de base de l`algèbre

1. Réviser les compétences de base en mathématiques. Pour apprendre l`algèbre, vous aurez besoin de connaître les compétences de base telles que l`addition, la soustraction, la multiplication et la division. Ces compétences en mathématiques que vous apprenez à l`école primaire sont essentielles avant de commencer l`algèbre. Si vous ne maîtrisez pas ces compétences, il sera difficile d`apprendre les concepts plus complexes abordés en algèbre. Si vous avez besoin d`un rappel sur ces opérations, consultez wikiHow pour des articles sur les bases des mathématiques.
- Il n`est pas nécessaire d`être très bon en calcul mental si l`on veut bien faire de l`algèbre. Vous serez souvent autorisé à travailler avec une calculatrice pendant le cours de mathématiques, pour gagner du temps tout en faisant des calculs simples. Vous devriez dans tous les cas pouvoir faire des calculs sans calculatrice, au cas où vous ne seriez pas autorisé à l`utiliser.

2. Apprendre l`ordre des opérations. L`une des choses les plus difficiles lorsqu`il s`agit de résoudre une équation mathématique est de savoir par où commencer. Heureusement, il y a un certain ordre dans lequel vous résolvez ces problèmes : d`abord les termes sont entre parenthèses, puis les exposants/puissances, puis la multiplication, la division, l`addition et enfin la soustraction. Un mnémonique pratique pour se souvenir de la séquence d`opérations est « Comment devrions-nous nous débarrasser des éléments insuffisants » (ou comme acronyme HMWVDOA). Voir wikiHow pour les articles sur l`application de l`ordre des opérations. Pour rappel, voici à nouveau la séquence des opérations :

3. Apprenez à utiliser les nombres négatifs. Il est courant en algèbre d`utiliser des nombres négatifs, c`est donc une bonne idée de revoir comment additionner, soustraire, multiplier et diviser des nombres négatifs avant de passer à l`algèbre. Vous trouverez ci-dessous quelques notions de base pour travailler avec des nombres négatifs dont vous devrez vous souvenir — pour plus d`informations, consultez les articles de wikiHow sur l`addition, la soustraction, la division et la multiplication de nombres négatifs.

4. Apprenez à organiser de longs problèmes. Alors que les problèmes d`algèbre simples sont souvent faciles à résoudre, les problèmes plus complexes peuvent nécessiter de nombreuses étapes. Afin d`éviter les erreurs, commencez sur une nouvelle ligne chaque fois que vous faites un pas de plus dans la résolution du problème. Si vous avez affaire à une équation avec des termes des deux côtés du signe égal, essayez d`écrire ces signes (`=`) l`un en dessous de l`autre. De cette façon, toute erreur dans votre calcul sera beaucoup plus facile à détecter.
- 9/3 - 5 + 3×4
- 9/3 - 5 + 12
- 3 - 5 + 12
- 3 + 7
- dix
Partie 2 sur 5: Comprendre les variables

1. Recherchez des symboles qui ne sont pas des nombres. En algèbre, vous traiterez des lettres et des symboles dans vos problèmes de mathématiques, plutôt que des chiffres. C`est ce qu`on appelle des variables. Les variables ne sont pas aussi difficiles qu`elles le paraissent à première vue - ce ne sont que des moyens de représenter des nombres avec des valeurs inconnues. Voici quelques exemples courants de variables en algèbre :
- Des lettres comme x, y, z, a, b et c
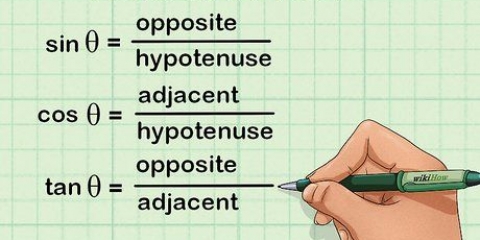
- Lettres grecques telles que thêta, ou θ
- Notez que non tout les symboles sont des variables inconnues. Par exemple : pi ou π, toujours égal (arrondi au supérieur) 3,1459.

2. Considérez les variables comme des nombres « inconnus ». Comme mentionné ci-dessus, les variables ne sont généralement que des nombres avec des valeurs inconnues. En d`autres termes, il y a un numéro qui peut remplacer la variable pour faire fonctionner l`équation. Habituellement, le but d`un problème d`algèbre est de comprendre quelle est cette variable - pensez-y comme un "nombre mystérieux" que vous essayez de découvrir.

3. Si une variable apparaît plusieurs fois, simplifiez les variables. Que faire lorsque la même variable apparaît plusieurs fois dans une équation? Bien que cela puisse sembler une situation délicate, vous pouvez traiter les variables de la même manière que les nombres normaux - en d`autres termes, vous pouvez ajouter, soustraire, etc. tant que vous ne combinez que des variables identiques. En d`autres termes, x + x=2x, mais x + y n`est pas égal à 2xy.
Partie3 sur 5: Résoudre des équations en éliminant

1. Isoler la variable dans l`équation. Résoudre une équation en algèbre implique généralement d`essayer de déterminer quelle est la variable. Les équations algébriques ont généralement des nombres et/ou des variables des deux côtés, comme ceci : x + 2=9 × 4. Pour déterminer quelle est la variable, vous devrez la placer d`un côté du signe égal. Ce qui reste de l`autre côté du signe égal est la réponse.
- Dans l`exemple (x + 2=9 × 4), pour isoler x du côté gauche de l`équation, nous devons nous débarrasser du `+2`. Pour ce faire, nous soustrayons 2 de ce côté, laissant x=9 × 4. Pour que les deux côtés de l`équation soient égaux, nous devons également soustraire 2 de l`autre côté. Cela nous laisse avec x=9 × 4 – 2. Selon l`ordre des opérations, on multiplie d`abord, puis on soustrait et on obtient x=36 - 2=34.

2. Élimine l`addition par soustraction (et vice versa). Comme nous l`avons vu ci-dessus, isoler x d`un côté du signe égal implique généralement d`essayer de se débarrasser des nombres immédiatement adjacents. Pour ce faire, effectuez l`opération « opposée » des deux côtés de l`équation. Par exemple, dans l`équation x + 3=0, on met un `- 3` des deux côtés, car il y a un `+ 3` à côté du x. Faire cela isolera x et obtiendra `-3` de l`autre côté du signe égal, comme ceci : x=-3.
- Lors de l`addition, la soustraction. Exemple : x + 9=3 → x=3 - 9
- Lors de la soustraction, l`ajout. Exemple : x - 4=20 → x=20 + 4

3. Élimine la multiplication en divisant (et vice versa). La multiplication et la division sont un peu plus difficiles à travailler que l`addition et la soustraction, mais elles ont la même relation « opposée ». Si vous voyez un `×3` sur un côté, vous pouvez l`éliminer en divisant les deux côtés par 3.
- En multipliant, en divisant. Exemple : 6x=14 + 2→ x=(14 + 2)/6
- En divisant, en multipliant. Exemple : x/5=25 → x=25 × 5

4. Éliminer les exposants en prenant des racines carrées (et vice versa). Les exposants sont un sujet avancé en algèbre — si vous ne savez pas quoi en faire, lisez l`article de wikiHow pour débutants sur les exposants. Le « opposé » d`un exposant est la racine de la puissance de ce nombre. Par exemple, l`opposé de l`exposant est la racine carrée (√), l`opposé de l`exposant est la racine cubique (√), etc.
- Pour les exposants, prendre la racine carrée. Exemple : x=49 → x=√49
- Pour les racines, prenez l`exposant. Exemple : √x=12 → x=12
Partie 4 sur 5: Aiguiser vos compétences en mathématiques

1. Utiliser des images pour rendre les problèmes plus clairs. Si vous êtes incapable de représenter un problème d`algèbre, utilisez des graphiques ou des images pour illustrer l`équation. Vous pouvez même utiliser un groupe d`objets (comme des blocs ou des pièces) si vous les avez à portée de main.
- Par exemple, résolvons l`équation x + 2=3 en utilisant des cases (☐)
- x +2=3
- +☐☐=☐☐☐
- À ce stade, soustrayez 2 des deux côtés, en supprimant 2 carrés (☐☐) de chaque côté :
- +☐☐-☐☐=☐☐☐-☐☐
- =☐, ou x=1
- Autre exemple : 2x=4
- =☐☐☐☐
- À ce stade, nous divisons les deux côtés par deux, en divisant les cases des deux côtés en deux groupes :
- |☒=☐☐|☐☐
- =☐☐, ou x=2

2. Utilisez des « contrôles logiques » (surtout en cas de problèmes). Lorsque vous devez convertir un problème en une équation algébrique, vérifiez votre formule en traitant des valeurs simples dans les variables. Votre équation est-elle correcte lorsque x=0? Quand x=1? Quand x=-1? Il est facile de faire de petites erreurs en notant quelque chose comme p=6d quand vous voulez dire p=d/6, mais vous les repérerez assez rapidement si vous vérifiez le travail que vous avez fait avant de continuer.

3. Gardez à l`esprit que les réponses ne sont pas toujours des nombres entiers en mathématiques. Les réponses en algèbre et dans d`autres branches des mathématiques ne sont pas toujours des nombres ronds et faciles. Ce sont souvent des nombres décimaux, des fractions ou des nombres irrationnels. Une calculatrice peut vous aider à trouver ces réponses compliquées, mais gardez à l`esprit que votre professeur peut vous demander de donner la réponse exacte, et non avec une décimale maladroite.

4. Si vous connaissez les bases de l`algèbre, essayez l`affacturage. L`une des compétences les plus délicates en algèbre est la factorisation - une sorte de raccourci pour écrire des équations complexes sous une forme plus simple. L`affacturage est un sujet assez avancé en algèbre, alors consultez l`article lié ci-dessus si vous le trouvez difficile. Voici quelques conseils pour vous aider à factoriser les équations :

5. Pratique, pratique, pratique! La progression dans l`apprentissage de l`algèbre (et de toute autre branche des mathématiques) nécessite beaucoup de travail acharné et de répétition. Ne vous inquiétez pas - en faisant attention en classe, en faisant tous vos devoirs et en demandant l`aide de votre professeur ou d`autres étudiants en cas de besoin, l`algèbre finira par devenir une seconde nature.

6. Demandez à votre professeur de vous aider avec les matières les plus difficiles. Si vous avez du mal à maîtriser le matériel, ne vous inquiétez pas - vous n`avez pas à l`apprendre par vous-même. Votre professeur est la première personne à vous aider avec des questions. Après le cours, demandez poliment de l`aide au professeur. Les bons enseignants sont généralement disposés à réexpliquer un sujet lorsque vous leur rendez visite après la classe, et peuvent même être en mesure de vous fournir du matériel de pratique supplémentaire.
Partie5 sur 5:Exploration de sujets avancés

1. Apprendre à tracer une équation. Les graphiques sont des outils précieux en algèbre car ils vous permettent de représenter des idées qui nécessitent généralement des nombres dans des images faciles à comprendre. Habituellement, lorsque vous commencez avec l`algèbre, les graphiques sont limités aux problèmes d`équations à deux variables (généralement x et y) et sont représentés dans un simple graphique 2D avec un axe x et un axe y. Avec ces équations, tout ce que vous avez à faire est de brancher une valeur pour x, puis de résoudre pour y (ou vice versa) pour obtenir deux nombres qui correspondent à un point sur le graphique.
- Par exemple, dans l`équation y=3x, nous substituons 2 pour x, et nous obtenons y=6 comme réponse. Cela signifie que le point (2.6) (deux points à droite du point zéro et 6 vers le haut) fait partie du graphique de l`équation.
- Les équations de la forme y=mx + b (où m et b sont des nombres) sont spécial juste dans les bases de l`algèbre. Ces équations ont toujours une pente m et coupent l`axe des y au point y=b.

2. Apprendre à résoudre les inégalités. Que faire quand une équation n`a pas de signe égal? Rien de spécial par rapport à ce que tu ferais différemment, s`avère. Dans les inégalités, où vous rencontrez des signes comme, > ("supérieur à") et< ("moins de"), résolvez l`équation de la même manière que précédemment. La réponse que vous obtenez est soit plus petite soit plus grande que votre variable.
- 3 > 5x - 2
- 5 > 5x
- 1 > x, ou X< 1.

3. Résoudre des équations quadratiques ou quadratiques. Un sujet algébrique sur lequel de nombreux débutants trébuchent est la résolution d`équations quadratiques. Ce sont des équations de la forme ax + bx + c=0, où a, b et c sont des nombres (sauf que a ne peut pas être 0). Nous résolvons ces équations avec la formule x=[-b +/- √(b - 4ac)]/2a . Soyez prudent - le +/- signifie que vous devez trouver les réponses pour les deux additions si soustraire, de sorte qu`il y a deux réponses possibles pour ce type de problème.
- x=[-b +/- (b - 4ac)]/2a
- x=[-2 +/- (2 - 4(3)(-1))]/2(3)
- x=[-2 +/- (4 - (-12))]/6
- x=[-2 +/- (16)]/6
- x=[-2 +/- 4]/6
- x=-1 et 1/3

4. Expérimenter avec le système d`équations. Résoudre plusieurs équations à la fois peut sembler très délicat, mais si vous travaillez avec des équations algébriques simples, ce n`est pas si difficile. Souvent, les professeurs de mathématiques utilisent un graphique pour résoudre ces problèmes. Si vous travaillez avec des systèmes de deux équations, vous trouverez la solution en regardant les points du graphique où les droites des deux équations se coupent.
- y=3x - 2
- -5=3(-1) - 2
- -5=-3 - 2
- -5=-5
- y=-x - 6
- -5=-(-1) - 6
- -5=1 - 6
- -5=-5
Des astuces
- Il existe des tonnes de ressources pour les personnes qui souhaitent apprendre l`algèbre en ligne. Une simple recherche dans un moteur de recherche comme « aide à l`algèbre » peut donner des dizaines d`excellents résultats. Jetez également un œil à la catégorie Mathématiques. Vous y trouverez beaucoup d`informations, alors commencez tout de suite!
- Un excellent site pour les débutants en algèbre est khanacademy.com. Ce site gratuit propose de nombreuses leçons faciles à suivre sur un large éventail de sujets, y compris l`algèbre. Il y a des vidéos sur tout, des sujets extrêmement simples aux sujets de niveau universitaire, alors n`hésitez pas à profiter de Khan Academy et de toute l`aide que ce site peut vous apporter!
- N`oubliez pas que les meilleures ressources pour apprendre l`algèbre sont les personnes que vous connaissez déjà. Consultez des amis ou d`autres étudiants de la même classe si vous avez besoin d`aide sur des sujets abordés en classe.
Articles sur le sujet "Apprendre l'algèbre"
Оцените, пожалуйста статью
Populaire