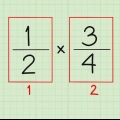
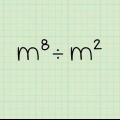Par exemple : la fraction  pouvez-vous simplifier à
pouvez-vous simplifier à  . Alors,
. Alors, 

Par exemple : parce que  , pouvez-vous réécrire l`expression exponentielle comme
, pouvez-vous réécrire l`expression exponentielle comme  .
. 
Par exemple:  .
. 
Par exemple : parce que ![Résolution des exposants décimaux 81^{{{frac{1}{4}}}}={sqrt[ {4}]{81}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b37415d73d383d0450962dda1cf0ddb2e0da0452) , pouvez-vous réécrire l`équation comme
, pouvez-vous réécrire l`équation comme ![Résolution des exposants décimaux ({sqrt[ {4}]{81}})^{{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79a4e12743be369be81296fe2aeabd97c70cb9ab) .
. 
Par exemple : Om ![Résolution des exposants décimaux {sqrt[ {4}]{81}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44f5722ccf46fec0200534e84bda483bc2b726b1) pour calculer, vous devez déterminer quel nombre multiplié par quatre est égal à 81. Parce que
pour calculer, vous devez déterminer quel nombre multiplié par quatre est égal à 81. Parce que  , sais-tu
, sais-tu ![Résolution des exposants décimaux {sqrt[ {4}]{81}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/44d91764f62522cec7024ef6481f0b83305f17e9) . Ainsi, l`équation exponentielle devient maintenant
. Ainsi, l`équation exponentielle devient maintenant  .
. 
Par exemple:  . Alors,
. Alors,  .
. 

La décimale  est égal à
est égal à  , Alors
, Alors  .
. 
Parce que  est simplifié à
est simplifié à  , cela compte-t-il
, cela compte-t-il  .
. Si vous convertissez ceci en une fraction impropre, vous obtenez  . Alors,
. Alors,  .
. 






Par exemple:  .
. 
Par exemple:  .
. 
![Résolution des exposants décimaux x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
![Résolution des exposants décimaux x^{{{frac{1}{4}}}}={sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/625ea5fe7631555b2fc23ac21f595d7c20633ec9)
![Résolution des exposants décimaux x^{{{frac{1}{5}}}}={sqrt[ {5}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/788c8c448ea3cf9b81867b10ba6bbb1a47abb388)
Par exemple: ![Résolution des exposants décimaux 81^{{{frac{1}{4}}}}={sqrt[ {4}]{81}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/0af496f05893da79ec2c45b4ebebabce0930dce0) . Vous savez que trois est la quatrième racine de 81 parce que
. Vous savez que trois est la quatrième racine de 81 parce que 

Si vous avez affaire à des exposants de racine carrée, alors cette loi devient  , parce que
, parce que  .
.
Résolution des exposants décimaux
Teneur
Le calcul des exposants est une compétence de base que les étudiants apprennent en pré-algèbre. Habituellement, vous voyez les exposants comme des nombres entiers et parfois vous les voyez comme des fractions. Vous les voyez rarement comme des décimales. Lorsqu`un exposant est affiché sous forme de nombre décimal, vous devez convertir le nombre décimal en fraction. Ensuite, il existe des règles et des lois concernant les exposants que vous pouvez utiliser pour calculer l`expression.
Pas
Partie 1 sur 3: Calcul d`un exposant décimal

1. Convertir le nombre décimal en fraction. Pour convertir un nombre décimal en fraction, il faut considérer la valeur de position. Le dénominateur de la fraction est la valeur de position. Les chiffres de la virgule sont égaux au numérateur.
- Par exemple : pour l`expression exponentielle
, Dois tu
convertir en fraction. Puisque la décimale va à la place des centièmes, la fraction correspondante est
.

2. Simplifier la fraction, si possible. Puisque vous prenez une racine qui correspond au dénominateur de la fraction de l`exposant, vous voulez que le dénominateur soit le plus petit possible. Faites ceci simplification de la pause. Si la fraction est un nombre fractionnaire (d.w.z. si votre exposant est un nombre décimal supérieur à 1), réécrivez-le comme une fraction impropre.
 pouvez-vous simplifier à
pouvez-vous simplifier à  . Alors,
. Alors, 

3. Réécrire l`exposant sous forme de multiplication. Vous faites cela en faisant du numérateur un entier et en le multipliant par la fraction radicale. La fraction racine est la fraction avec le même dénominateur, mais avec 1 comme numérateur.
 , pouvez-vous réécrire l`expression exponentielle comme
, pouvez-vous réécrire l`expression exponentielle comme  .
.
4. Réécrire l`exposant comme une puissance d`une puissance. Rappelez-vous que multiplier deux exposants équivaut à la puissance d`une puissance. Alors  devient
devient  .
.
 devient
devient  .
. .
.
5. Réécrire la base sous la forme d`une équation de racine carrée. Calculer l`exposant d`un nombre équivaut à calculer une racine appropriée de ce nombre. Réécrivez donc la base et le premier exposant sous la forme d`une équation de racine carrée.
![Résolution des exposants décimaux 81^{{{frac{1}{4}}}}={sqrt[ {4}]{81}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b37415d73d383d0450962dda1cf0ddb2e0da0452) , pouvez-vous réécrire l`équation comme
, pouvez-vous réécrire l`équation comme ![Résolution des exposants décimaux ({sqrt[ {4}]{81}})^{{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79a4e12743be369be81296fe2aeabd97c70cb9ab) .
.
6. Calculer l`équation de la racine carrée. N`oubliez pas que l`exposant racine (le petit nombre en dehors du radical) vous indique quelle racine vous recherchez. Si les chiffres sont difficiles, il est préférable de le faire avec le ![Résolution des exposants décimaux {sqrt[ {x}]{y}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58c28156258e3c4cf15e8af14abcc0163150e3e6) fonction sur une calculatrice mathématique.
fonction sur une calculatrice mathématique.
![Résolution des exposants décimaux {sqrt[ {x}]{y}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58c28156258e3c4cf15e8af14abcc0163150e3e6) fonction sur une calculatrice mathématique.
fonction sur une calculatrice mathématique.![Résolution des exposants décimaux {sqrt[ {4}]{81}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44f5722ccf46fec0200534e84bda483bc2b726b1) pour calculer, vous devez déterminer quel nombre multiplié par quatre est égal à 81. Parce que
pour calculer, vous devez déterminer quel nombre multiplié par quatre est égal à 81. Parce que  , sais-tu
, sais-tu ![Résolution des exposants décimaux {sqrt[ {4}]{81}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/44d91764f62522cec7024ef6481f0b83305f17e9) . Ainsi, l`équation exponentielle devient maintenant
. Ainsi, l`équation exponentielle devient maintenant  .
.
sept. Calculer l`exposant restant. Vous devriez maintenant avoir un nombre entier comme exposant, donc le calcul devrait être simple sinon. Vous pouvez toujours utiliser une calculatrice si les nombres sont trop gros.
 . Alors,
. Alors,  .
.Partie 2 sur 3: Résoudre un exemple de problème

1. Calculez l`équation exponentielle suivante : .
.
 .
.
2. Convertir le nombre décimal en fraction. Parce que  est supérieur à 1, la fraction est un nombre fractionnaire.
est supérieur à 1, la fraction est un nombre fractionnaire.
 est supérieur à 1, la fraction est un nombre fractionnaire.
est supérieur à 1, la fraction est un nombre fractionnaire. est égal à
est égal à  , Alors
, Alors  .
.
3. Simplifier la fraction, si possible. Vous devez également convertir tout nombre mixte en fractions impropres.
 est simplifié à
est simplifié à  , cela compte-t-il
, cela compte-t-il  .
. . Alors,
. Alors,  .
.
4. Réécrire l`exposant sous forme de multiplication. Parce que  , pouvez-vous réécrire l`équation comme
, pouvez-vous réécrire l`équation comme  .
.
 , pouvez-vous réécrire l`équation comme
, pouvez-vous réécrire l`équation comme  .
.
5. Réécrire l`exposant comme une puissance d`une puissance. Alors,  .
.
 .
.
6. Réécrire la base sous la forme d`une équation de racine carrée.![Résolution des exposants décimaux 256^{{{frac{1}{4}}}}={sqrt[ {4}]{256}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb9c02c237d2aeb16bc1fd12eaf89cbde1d683a4) , qui permet de réécrire l`équation sous la forme
, qui permet de réécrire l`équation sous la forme ![Résolution des exposants décimaux ({sqrt[ {4}]{256}})^{{9}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/261990049bf6155622a73330e280af3d17084588) .
.
![Résolution des exposants décimaux 256^{{{frac{1}{4}}}}={sqrt[ {4}]{256}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb9c02c237d2aeb16bc1fd12eaf89cbde1d683a4) , qui permet de réécrire l`équation sous la forme
, qui permet de réécrire l`équation sous la forme ![Résolution des exposants décimaux ({sqrt[ {4}]{256}})^{{9}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/261990049bf6155622a73330e280af3d17084588) .
.
sept. Calculer l`équation de la racine carrée.![Résolution des exposants décimaux {sqrt[ {4}]{256}}=4](https://wikimedia.org/api/rest_v1/media/math/render/svg/55bb3e8f3f86ce5c35d5f18ddd8f486e75e67476) . L`équation est donc maintenant
. L`équation est donc maintenant  .
.
![Résolution des exposants décimaux {sqrt[ {4}]{256}}=4](https://wikimedia.org/api/rest_v1/media/math/render/svg/55bb3e8f3f86ce5c35d5f18ddd8f486e75e67476) . L`équation est donc maintenant
. L`équation est donc maintenant  .
.
8. Calculer l`exposant restant. . Alors,
. Alors,  .
.
 . Alors,
. Alors,  .
.Partie3 sur 3: Comprendre les exposants

1. Reconnaître une équation exponentielle. Une équation exponentielle a une base et un exposant. La base est le plus grand nombre dans l`équation. L`exposant est le plus petit nombre.
- Par exemple : dans l`équation
, est
la base et
l`exposant.

2. Reconnaître les parties d`une équation exponentielle. La base est le nombre multiplié. L`exposant indique à quelle fréquence la base est utilisée comme facteur dans l`équation.
 .
.
3. Reconnaître un exposant racine carrée. Un exposant de racine carrée peut également être appelé un exposant de fraction. C`est un exposant sous la forme d`une fraction.
 .
.
4. Comprendre la relation entre la racine carrée et les exposants de racine carrée. l`exaltation  d`un nombre est comme la racine carrée de ce nombre. Alors,
d`un nombre est comme la racine carrée de ce nombre. Alors,  . Il en va de même pour les autres racines et exposants. Le dénominateur de l`exposant vous indique quelle racine prendre :
. Il en va de même pour les autres racines et exposants. Le dénominateur de l`exposant vous indique quelle racine prendre :
 d`un nombre est comme la racine carrée de ce nombre. Alors,
d`un nombre est comme la racine carrée de ce nombre. Alors,  . Il en va de même pour les autres racines et exposants. Le dénominateur de l`exposant vous indique quelle racine prendre :
. Il en va de même pour les autres racines et exposants. Le dénominateur de l`exposant vous indique quelle racine prendre :![Résolution des exposants décimaux x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
![Résolution des exposants décimaux x^{{{frac{1}{4}}}}={sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/625ea5fe7631555b2fc23ac21f595d7c20633ec9)
![Résolution des exposants décimaux x^{{{frac{1}{5}}}}={sqrt[ {5}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/788c8c448ea3cf9b81867b10ba6bbb1a47abb388)
![Résolution des exposants décimaux 81^{{{frac{1}{4}}}}={sqrt[ {4}]{81}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/0af496f05893da79ec2c45b4ebebabce0930dce0) . Vous savez que trois est la quatrième racine de 81 parce que
. Vous savez que trois est la quatrième racine de 81 parce que 

5. Comprendre la loi exponentielle de puissance d`une puissance. Cette loi stipule que  . En d`autres termes, élever un exposant à la puissance revient à multiplier deux exposants.
. En d`autres termes, élever un exposant à la puissance revient à multiplier deux exposants.
 . En d`autres termes, élever un exposant à la puissance revient à multiplier deux exposants.
. En d`autres termes, élever un exposant à la puissance revient à multiplier deux exposants. , parce que
, parce que  .
.Articles sur le sujet "Résolution des exposants décimaux"
Оцените, пожалуйста статью
Populaire