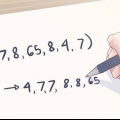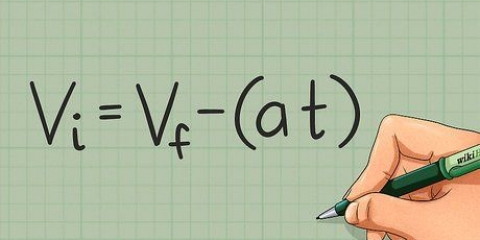Comment déterminer la précision

Teneur

Pas
Des astuces

La précision signifie qu`une mesure avec un outil ou un instrument particulier produit des résultats similaires à chaque fois qu`il est utilisé. Par exemple, si vous montez sur une balance cinq fois de suite, une balance précise devrait vous montrer le même poids à chaque fois. En mathématiques et en sciences, la précision du calcul est essentielle pour déterminer si vos instruments et mesures sont suffisamment bons pour obtenir de bonnes données. Vous pouvez représenter la précision de chaque ensemble de données en utilisant la plage des valeurs, l`écart moyen ou l`écart type.

Pas

Méthode 1 sur 4: Calcul de la plage

Image intitulée Calculer la précision Étape 1

1. Déterminer la valeur mesurée la plus élevée. Il est utile de commencer à trier vos données par ordre numérique, du plus bas au plus élevé. Cela garantira que vous ne sautez aucune des valeurs. Sélectionnez ensuite la valeur à la fin de la liste.

Par exemple, supposons que vous testiez la précision d`une balance et que vous voyiez cinq lectures : 11, 13, 12, 14, 12. Triées ces valeurs sont affichées comme 11, 12, 12, 13, 14. La valeur la plus élevée est 14.

Image intitulée Calculer la précision, étape 2

2. Déterminer la valeur mesurée la plus basse. Une fois vos données triées, trouver la valeur la plus basse est aussi simple que de regarder le début de la liste.

Dans les données de mesure de l`échelle, la valeur la plus basse est 11.

Image intitulée Calculer la précision Étape 3

3. Soustraire la valeur la plus faible de la plus élevée. La plage d`un ensemble de données est la différence entre les lectures les plus élevées et les plus basses. Il suffit de soustraire les uns des autres. Algébriquement, l`étendue est exprimée par :

intervalle = X (m une X) - X (m je m)

${text{Plage}}=x(max)-x(min)$

La plage des exemples de données est :

intervalle = X (m une X) - X (m je m) = 14 - 11 = 3

${text{Plage}}=x(max)-x(min)=14-11=3$

Image intitulée Calculer la précision, étape 4

4. Afficher la plage comme la précision. Lorsque vous rapportez des données, il est important que les lecteurs sachent ce que vous avez mesuré. Étant donné que la précision dépend de différentes métriques, vous devez spécifier ce que vous souhaitez signaler. Pour ces données, vous indiquez : moyenne = 12,4, plage = 3. Ou simplement : moyenne = 12,4 ±3.

La moyenne ne fait pas nécessairement partie du calcul de la plage ou de la précision, mais est généralement le premier calcul pour rapporter la valeur mesurée. La moyenne est obtenue en divisant la somme des valeurs mesurées par le nombre d`éléments du groupe. La moyenne de cette série de données est (11 + 13 + 12 + 14 + 12) / 5 = 12,4.

Méthode 2 sur 4 : Calcul de l`écart moyen

Image intitulée Calculer la précision étape 5

1. Déterminer d`abord la moyenne des données. L`écart moyen est une mesure plus détaillée de la précision d`un groupe de mesures ou de valeurs d`une expérience. La première étape pour trouver l`écart moyen consiste à calculer la moyenne des valeurs mesurées. La moyenne est la somme des valeurs divisée par le nombre de mesures.

Dans cet exemple, nous utilisons les mêmes exemples de données qu`auparavant. Supposons que cinq mesures ont été prises, 11, 12, 13, 14 et 12. La moyenne de ces valeurs est (11 + 13 + 12 + 14 + 12) / 5 = 12,4.

Image intitulée Calculer la précision étape 6

2. Calculer l`écart absolu de chaque valeur par rapport à la moyenne. Pour ce calcul de précision, vous devez déterminer à quel point chaque valeur est proche de la moyenne. Pour ce faire, soustrayez la moyenne de chaque nombre. Pour cette mesure, peu importe que la valeur soit supérieure ou inférieure à la moyenne. Soustrayez les nombres et utilisez simplement la valeur positive du résultat. Ceci est également connu sous le nom de « valeur absolue ».

Algébriquement, la valeur absolue est représentée en plaçant deux barres verticales autour du calcul. Comme suit:

Déviation absolue = | X - ?? |

${text{Déviation absolue}}=|x-mu |$

Ce calcul indique

X

$X$ pour chacune des valeurs expérimentales et

??

$mu$ pour la moyenne calculée.

En ce qui concerne les valeurs de la série de données d`échantillon, les écarts absolus sont :

| 12 - 12, 4 | = 0, 4

$|12-12.4|=0.4$

| 11 - 12, 4 | = 1, 4

$|11-12.4|=1.4$

| 14 - 12, 4 | = 1, 6

$|14-12,4|=1,6$

| 13 - 12, 4 | = 0, 6

$|13-12.4|=0.6$

| 12 - 12, 4 | = 0, 4

$|12-12.4|=0.4$

Image intitulée Calculer la précision Étape 7

3. Déterminer l`écart moyen. Utiliser les écarts absolus et trouver leur moyenne. Comme avec l`ensemble de données d`origine, vous additionnez les valeurs et divisez la somme par le nombre de valeurs. Ceci est représenté algébriquement par :

Écart moyen = ?? | X - ?? | m

${text{Mean Deviation}}={frac{Sigma |x-mu |}{n}}$

En ce qui concerne cet exemple de données, le calcul se déroule comme suit :

Écart moyen = 0, 4 + 1, 4 + 1, 6 + 0, 6 + 0, 4 5

${text{Déviation moyenne}}={frac{0,4+1,4+1,6+0,6+0,4}{5}}$

Écart moyen = 4, 4 5

${text{Déviation moyenne}}={frac{4,4}{5}}$

Écart moyen = 0, 88

${text{Déviation moyenne}}=0.88$

Image intitulée Calculer la précision à l`étape 8

4. Donner le résultat de l`exactitude. Ce résultat peut être rapporté comme la moyenne, plus ou moins l`écart moyen. Pour cet exemple d`ensemble de données, cela ressemble à 12,4 ± 0,88. Notez qu`en indiquant la précision comme écart moyen, la mesure semble beaucoup plus précise qu`avec la plage.

Méthode 3 sur 4: Calculer l`écart type

Image intitulée Calculate Precision Step 9

1. Utiliser la formule correcte pour l`écart type. Quelle que soit la taille de l`ensemble de données, l`écart type est une statistique fiable pour afficher la précision. Il existe deux formules pour calculer l`écart type, avec une très petite différence entre elles. Vous utilisez une formule si vos métriques couvrent une population entière. La deuxième formule est utilisée si les données mesurées ne sont qu`un échantillon de la population.

Vos données représentent une population entière si vous avez collecté toutes les mesures possibles de tous les sujets possibles. Par exemple, si vous testez des personnes atteintes d`une maladie très rare et que vous êtes sûr d`avoir testé toutes les personnes atteintes de cette maladie, cela inclut l`ensemble de la population. La formule de l`écart type dans ce cas est :

$?? = \sqrt{} ?? (X - ??) 2 m$ $sigma ={sqrt{{frac{Sigma (x-mu )^{2}}{n}}}}$

Un échantillon est un groupe de données plus petit qu`une population entière. Vous utiliserez généralement celui-ci le plus. La formule d`écart type pour un échantillon est :

?? = \sqrt{} ?? (X - ??) 2 m - 1

$sigma ={sqrt{{frac{Sigma (x-mu )^{2}}{n-1}}}}$

Notez que la seule différence est le dénominateur de la fraction. Pour une population complète, diviser par

m

$m$ . Si vous avez un échantillon, merci de partager

m - 1

$n-1$ .

Image intitulée Calculer la précision de l`étape 10

2. Trouver la moyenne des valeurs des données. Comme pour le calcul de l`écart moyen, vous commencez par déterminer la moyenne des valeurs de données.

En utilisant le même ensemble de lectures que celui indiqué ci-dessus, la moyenne est de 12,4.

Image intitulée Calculer la précision Étape 11

3. Trouver le carré de chaque variante. Pour chaque point de données, soustrayez la valeur des données de la moyenne et placez le résultat au carré. Puisque vous mettez ces variations au carré, peu importe que la différence soit positive ou négative. Le carré de la différence est toujours positif.

Pour les cinq valeurs de données de cet exemple, ces calculs se déroulent comme suit :

(12 - 12, 4) 2 = (- 0, 4)^{2} = 0, 16

$(12-12,4)^{2}=(-0,4)^{2}=0,16$

(11 - 12, 4) 2 = (- 1, 4)^{2} = 1, 96

$(11-12,4)^{2}=(-1,4)^{2}=1,96$

(14 - 12, 4) 2 = 1, 6^{2} = 2, 56

$(14-12,4)^{2}=1,6^{2}=2,56$

(13 - 12, 4) 2 = 0, 6^{2} = 0, 36

$(13-12,4)^{2}=0,6^{2}=0,36$

(12 - 12, 4) 2 = (- 0, 4)^{2} = 0, 16

$(12-12,4)^{2}=(-0,4)^{2}=0,16$

Image intitulée Calculate Precision Step 12

4. Calculer la somme des différences au carré. Le numérateur de la fraction dans l`écart type est la somme des différences au carré entre les valeurs et la moyenne. Vous pouvez déterminer ce montant en additionnant les nombres du calcul précédent.

Pour l`exemple d`ensemble de données, il s`agit de :

0, 16 + 1, 96 + 2, 56 + 0, 36 + 0, 16 = 5, 2

$0,16+1,96+2,56+0,36+0,16=5,2$

Image intitulée Calculate Precision Step 13

5. Diviser par la taille des données. C`est la seule étape qui est différente dans un calcul de population par rapport à un échantillon. Pour une population complète, vous divisez par

m

$m$ (le nombre de valeurs). Dans un échantillon, vous divisez par

m - 1

$n-1$ .

L`exemple suivant n`a que cinq mesures et n`est donc qu`un échantillon. Donc pour les cinq valeurs utilisées, diviser par (5 - 1) ou 4. Le résultat est

5, 2 / 4 = 1, 3

$5.2/4=1,3$ .

Image intitulée Calculer la précision à l`étape 14

6. Trouver la racine carrée du résultat. À ce stade, le calcul représente ce qu`on appelle la variance de l`ensemble de données. L`écart type est la racine carrée de la variance. Utilisez une calculatrice pour trouver la racine carrée, et avec elle l`écart type.

?? = \sqrt{1.3} = 1, 14

$sigma ={sqrt{1.3}}=1,14$

Image intitulée Calculer la précision à l`étape 15

sept. Montrez votre résultat. A l`aide de ce calcul, la précision de l`échelle peut être indiquée en indiquant la moyenne plus ou moins l`écart type. Pour ces données, il devient 12,4 ± 1,14.

L`écart type est peut-être la mesure de précision la plus courante. Cependant, pour plus de clarté, c`est toujours une bonne idée d`utiliser une note de bas de page ou des parenthèses pour indiquer que la valeur de précision représente l`écart type.

Méthode 4 sur 4: Décider comment déclarer l`exactitude

Image intitulée Calculer la précision à l`étape 16

1. Utilisez le mot précision correctement. La précision est un terme utilisé pour indiquer la répétabilité des mesures. Si vous collectez un groupe de données, soit par mesure, soit par le biais d`une expérience particulière, la précision décrit à quel point les résultats de chaque mesure ou expérience seront rapprochés.

La précision n`est pas la même chose que la précision. La précision mesure la proximité des valeurs expérimentales par rapport à la valeur réelle ou théorique, tandis que la précision mesure la proximité des valeurs mesurées les unes par rapport aux autres.
Les données peuvent être exactes mais pas exactes ou exactes mais pas exactes. Des lectures précises peuvent être proches de la cible, mais peuvent ne pas être proches les unes des autres. Les lectures précises sont proches les unes des autres, qu`elles soient ou non proches des valeurs cibles.

Image intitulée Calculer la précision Étape 17

2. Choisissez le meilleur degré de précision. Le mot `précision` n`a pas un sens unique. Il est possible d`afficher la précision avec plusieurs mesures différentes. Vous devrez décider lequel est le meilleur.

Varier. Pour les petits ensembles de données avec une dizaine de mesures ou moins, la plage de valeurs est une bonne mesure de précision. Cela est particulièrement vrai si les valeurs sont regroupées assez étroitement entre elles. Si vous trouvez qu`une ou deux valeurs sont éloignées des autres valeurs, alors vous devriez probablement utiliser un calcul différent.

Écart moyen. L`écart moyen est une mesure plus précise de l`exactitude d`un petit ensemble de valeurs de données.

écart-type. L`écart type est peut-être la mesure de précision la plus reconnue. L`écart type peut être utilisé pour calculer la précision des mesures pour une population entière ou un échantillon de la population.

Image intitulée Calculer la précision de l`étape 18

3. Fournissez une représentation claire de vos résultats. Très souvent, les chercheurs rapporteront des données en donnant la moyenne de la valeur mesurée suivie du degré de précision. La précision est indiquée par le symbole `±`. Cela donne une indication de l`exactitude, mais cela n`explique pas clairement au lecteur si le nombre après le symbole « ± » est une plage, un écart type ou une autre mesure. Pour l`énoncer clairement, vous devez définir le niveau de précision que vous avez utilisé, soit dans une note de bas de page, soit sous forme de commentaire entre parenthèses.

Pour une série de données donnée, le résultat peut être affiché sous la forme 12,4 ±3. Cependant, une manière plus descriptive d`énoncer les mêmes données serait la suivante : « Moyenne = 12,4, Plage = 3.`

Des astuces

Si l`une des valeurs de l`échantillon est bien supérieure ou inférieure au reste de vos valeurs, n`excluez pas cette valeur de vos calculs. Même si c`était une erreur, cela reste des données et doit être utilisé pour un calcul correct.
Seules cinq valeurs ont été utilisées dans cet article par souci de simplicité mathématique. Dans une expérience réelle, vous devez utiliser plus de cinq métriques pour un calcul plus précis. Plus vous exécutez d`échantillons, plus précis.