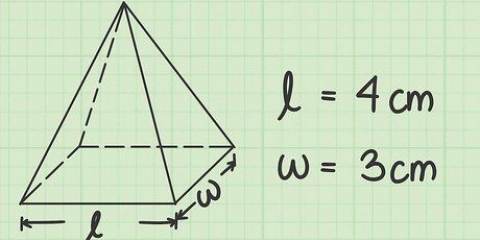Calcul du contenu

Teneur

Pas
Des astuces
Nécessités

Avez-vous déjà eu à remplir un bac à sable, un trou de poteau ou tout autre espace en trois dimensions ?? Ici, vous faites une "mesure cubique", un autre nom pour mesurer un volume. Pour calculer le volume d`un cube, d`un cylindre ou d`une sphère en mètres cubes, procédez comme suit.

Pas

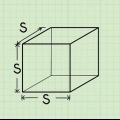
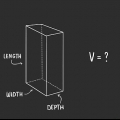
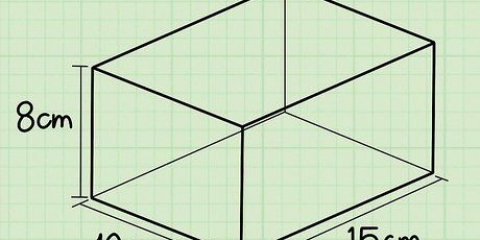
Méthode 1 sur 4: Carré ou rectangle

1. Mesurer la longueur de l`objet. Mesure en centimètres ou en mètres selon la taille.

Ex. 8 centimètres.

2. Mesurer la largeur de l`objet. Si vous avez utilisé des centimètres dans la mesure précédente, soyez cohérent et faites de même pour la largeur.

Ex. 16 centimètres.

3. Multiplier la longueur par la largeur. Calcule l`aire de la base de l`objet.

Ex. 8 centimètres x 16 centimètres = 128 centimètres carrés.

4. Mesurer la hauteur de l`objet. Notez ceci.

Ex. 27 centimètres.

5. Multipliez la base de l`objet (la surface.) avec la hauteur. Calculé le volume ou le volume d`un objet en trois dimensions.

Ex : 128 centimètres carrés x 27 centimètres = 3456 centimètres cubes.

6. Convertissez-le en mètres cubes si nécessaire.Pour convertir rapidement des centimètres cubes en mètres cubes, divisez le résultat par 1.000.000.

Ex. 3456 centimètres cubes / 1.000.000 = 0,003456 mètres cubes.

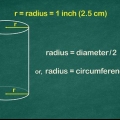
Méthode 2 sur 4: Le cylindre

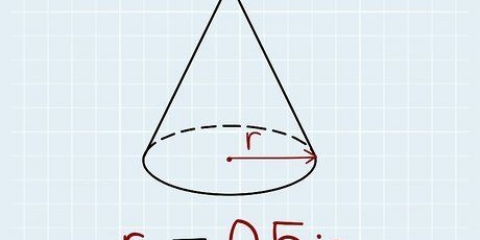
1. Mesurer le diamètre du cylindre et diviser par 2. La moitié de la largeur d`un cercle est aussi appelée Rayon ou rayon. Nous supposons que vous mesurez en centimètres.

Ex. 20 centimètres / 2 = 10 centimètres.

2. Multiplier le rayon par lui-même.C`est la même chose que le carré du rayon.

Ex. 10 centimètres x 10 centimètres = 100 centimètres carrés.

3. Multiplier le rayon au carré par pi. Si vous n`avez pas de bouton sur votre calculatrice pour pi (ou si vous pouvez travailler avec une estimation), multipliez par 3.14. Avec cela, vous avez calculé l`aire du cercle; la surface plane à l`extrémité du cylindre.

Ex. 100 centimètres x 3,14 = 314 centimètres carrés.

4. Mesurer la hauteur du cylindre. Vous pouvez également appeler cela la longueur, en fonction de l`orientation. Notez ce numéro.

Ex. 11 centimètres.

5. Multiplier l`aire de l`extrémité du cylindre par la hauteur. Avec cela vous connaissez le volume, ou aussi le volume du cylindre.

Ex. 314 centimètres carrés x 11 centimètres = 3454 centimètres cubes.

6. Convertissez la réponse en mètres cubes si nécessaire. Faites ceci comme mentionné précédemment.

Ex. 3454 centimètres cubes / 1.000.000 = 0,003454 mètres cubes.

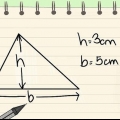
Méthode 3 sur 4: Pyramide à trois côtés

1. Mesurez un côté de la « base » de la pyramide. Mesurer la longueur d`un côté de la base triangulaire.

Ex. 9 centimètres.

2. Mesurer la « ligne d`altitude » de la base de la pyramide. C`est la distance d`un côté du triangle au point directement opposé à celui-ci.

Ex. 12 centimètres.

3. Multipliez la longueur du côté de la base par la hauteur et divisez par 2. Avec cela, vous avez calculé l`aire de la base triangulaire de la pyramide.

Ex. 9 centimètres x 12 centimètres = 108 centimètres carrés

108 centimètres carrés / 2 = 54 centimètres carrés

4. Mesurer la hauteur de la pyramide. Assurez-vous de mesurer dans une ligne verticale exacte de haut en bas, pas la diagonale de la pyramide. Notez ceci.

Ex. 32 centimètres.

5. Multiplier la surface de la base par la hauteur. Avec ça tu as calculé le volume (volume) d`une barre, pas encore celui de la pyramide!

Ex. 54 centimètres carrés x 32 centimètres = 1728 centimètres cubes.

6. Divisez le nombre précédent par trois. Il faut encore modifier le résultat précédent pour retrouver le contenu d`une pyramide. Pour ce faire, divisez le nombre précédent par trois. Ceci est valable pour toutes les pyramides.

Ex. 1728 centimètres cubes / 3 = 576 centimètres cubes.

sept. Convertissez-le en mètres cubes si nécessaire. Diviser par 1.000.000 pour faire ça.

Ex. 576 centimètres cubes / 1.000.000 = 0,000576 mètres cubes.

Méthode 4 sur 4: Pyramide à quatre côtés

1. Mesurer la longueur de la base de la pyramide en centimètres.

Ex. 8 centimètres.

2. Mesurez la largeur de la base de la pyramide, toujours en centimètres.

Ex. 18 centimètres.

3. Multiplier la longueur par la largeur. Calculer l`aire de la base de la pyramide.

Ex. 8 centimètres x 18 centimètres = 144 centimètres carrés.

4. Mesurer la hauteur de la pyramide. Assurez-vous de mesurer dans une ligne verticale exacte de haut en bas, pas la diagonale de la pyramide. Notez ceci.

Ex. 18 centimètres.

5. Multiplier la surface de la base par la hauteur. Avec ça tu as calculé le volume (volume) d`une barre, pas encore celui de la pyramide.

Ex. 144 centimètres carrés x 18 centimètres = 2592 centimètres cubes.

Ex. 2592 centimètres cubes / 3 = 864 centimètres cubes.

sept. Convertissez-le en mètres cubes si nécessaire. Diviser par 1.000.000 pour faire ça.

Ex. 864 centimètres cubes / 1.000.000 = 0,000864 mètres cubes.

Des astuces

Le terme « mètre cube » peut également être écrit sous la forme m^3 ; ne vous y trompez pas, c`est juste un raccourci pour "cubique", et pas quelque chose de nouveau.
Lors de la conversion de centimètres cubes en mètres cubes, il peut être utile d`utiliser environ 1.000.000 à considérer comme 100 x 100 x 100 ; il y a 100 centimètres dans un mètre, 100 x 100 dans un mètre carré et 100 x 100 x 100 dans un mètre cube.
L`idée de base du calcul dans l`espace tridimensionnel est de trouver le plan de la base et de le multiplier par la hauteur, ce qui vous donne trois dimensions. C`est bien sûr plus difficile avec des figures plus complexes ou irrégulières.