Diviser synthétiquement des polynômes : 12 étapes (avec des images)

Teneur

Pas
Des astuces

La division synthétique est une méthode abrégée de division de polynômes où vous divisez les coefficients des polynômes pour supprimer les variables et les exposants. Cela vous permet de travailler pendant ce calcul de la même manière qu`avec la division longue régulière. Si vous voulez savoir comment diviser synthétiquement des polynômes, suivez les étapes ci-dessous.

Pas

Image intitulée Diviser les polynômes à l`aide de la division synthétique Étape 1

1. Écrivez le problème. Par exemple, vous divisez x + 2x - 4x + 8 par x + 2. Écrivez la première équation quadratique, le dividende, au numérateur et la deuxième équation, le diviseur, au dénominateur.

Image intitulée Diviser les polynômes à l`aide de la division synthétique Étape 2

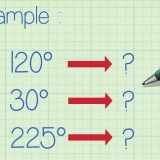
2. Inverser le signe de la constante dans le diviseur. La constante dans le diviseur, x + 2, est positive, donc l`inverse du signe de la constante est -2.

Image intitulée Diviser les polynômes à l`aide de la division synthétique Étape 3

3. Placez ce numéro à l`extérieur de la partie à l`extérieur du signe de division. Le signe de division ressemble à un arrière"je." Placez le terme -2 à gauche de ce symbole.

Image intitulée Diviser les polynômes à l`aide de la division synthétique, étape 4

4. Notez tous les coefficients du dividende dans le signe de division. Écrivez les termes de gauche à droite tels qu`ils apparaissent. Cela ressemble à ceci : -2| 12-48.

Image intitulée Diviser les polynômes à l`aide de la division synthétique, étape 5

5. Faire baisser le premier coefficient. Placer le premier coefficient, 1, en dessous de lui-même. Cela ressemble à ceci :

-2| 1 2 -4 8
??
1

Image intitulée Diviser les polynômes à l`aide de la division synthétique, étape 6

6. Multipliez le premier coefficient par le diviseur et placez-le en dessous du deuxième coefficient. Multipliez 1 par -2 et écrivez le produit -2 sous le deuxième terme, 2. Cela ressemble à ceci :

-2| 1 2 -4 8
-2
1

Image intitulée Diviser les polynômes à l`aide de la division synthétique Étape 7

sept. Additionnez le deuxième coefficient et écrivez la réponse sous le produit. Maintenant, prenez le deuxième coefficient, 2, et ajoutez-le à -2. Vous écrivez le résultat 0 sous les deux nombres, comme avec une division longue. Voilà à quoi ça ressemble :

-2| 1 2 -4 8
-2
dix

Image intitulée Diviser des polynômes à l`aide de la division synthétique, étape 8

8. Multipliez la somme par le diviseur et placez le résultat en dessous du troisième coefficient. Maintenant, prenez la somme 0 et multipliez-la par le diviseur -2. Placer le résultat 0 en dessous de 4, le troisième coefficient. Voilà à quoi ça ressemble :

-2| 1 2 -4 8
-2 0
1

Image intitulée Diviser les polynômes à l`aide de la division synthétique Étape 9

9. Additionnez le produit et le troisième coefficient et écrivez le résultat sous le produit. Ajoutez 0 à -4 et écrivez la réponse -4 en dessous de 0. Voici à quoi cela ressemble :

-2| 1 2 -4 8
-2 0
1 0 -4

Image intitulée Diviser les polynômes à l`aide de la division synthétique Étape 10

dix. Multipliez ce nombre par le diviseur, écrivez-le sous le dernier coefficient et ajoutez-le au coefficient. Multipliez maintenant -4 par -2 et écrivez la réponse 8 sous le quatrième coefficient, 8, et ajoutez ceci au quatrième coefficient. 8 + 8 = 16, c`est donc votre reste. Écrivez le numéro sous le produit. Voici à quoi cela ressemble :

-2| 1 2 -4 8
-2 0 8
1 0 -4 |16

Image intitulée Diviser les polynômes à l`aide de la division synthétique Étape 11

11. Placer chacun des nouveaux coefficients à côté d`une variable avec une puissance inférieure aux variables d`origine. Dans ce cas, la première somme, vaut 1, et est placée à côté d`un x élevé à la deuxième puissance (1 moins que 3). La deuxième somme, 0, est placée à côté d`un x, mais le résultat est 0, donc ce terme peut être supprimé. Et le troisième coefficient, -4, devient une constante, un nombre sans variable, car la variable d`origine était égale à x. Vous pouvez écrire un R à côté de 16, car c`est le reste. Voici à quoi cela ressemblera :

-2| 1 2 -4 8
-2 0 8
1 0 -4 |16
X + 0X - 4 R 16

X - 4R16

Image intitulée Diviser les polynômes à l`aide de la division synthétique Étape 12

12. Écrivez la réponse finale. C`est le nouveau polynôme, x - 4, plus le reste, 16 comme numérateur et x + 2 comme dénominateur. Voici à quoi cela ressemble : x - 4 +16/(x +2).

Des astuces

Pour vérifier votre réponse, multipliez le quotient par le diviseur et ajoutez le reste. Ce doit être le même que le polynôme d`origine.
(diviseur)(quotient)+(reste)
(X + 2)(X - 4) + 16
Multiplier par la première méthode externe, la dernière méthode interne.
(X - 4X + 2X - 8) + 16
X + 2X - 4X - 8 + 16
X + 2X - 4X + 8