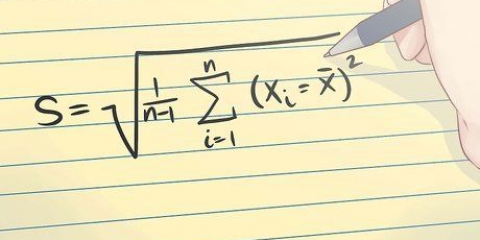En règle générale, le niveau de signification (ou alpha) est souvent fixé à 0,05, ce qui signifie que la probabilité d`observer accidentellement les différences présentes dans vos données n`est que de 5%. Un niveau de confiance plus élevé (et donc une valeur p plus faible) signifie que les résultats sont plus significatifs. Si vous souhaitez que les données soient plus fiables, définissez la valeur p inférieure à 0,01. Des valeurs p inférieures sont couramment utilisées dans l`industrie lors du débogage des produits. Il est très important de pouvoir avoir une grande confiance que chaque pièce fonctionne exactement comme il se doit. Pour la plupart des expériences vers une hypothèse, un niveau de signification de 0,05 est acceptable. 
Si vous ne savez pas si vos données sont supérieures ou inférieures au groupe de contrôle, utilisez un test à deux volets. Vous permet de tester la signification dans les deux sens. Si vous savez dans quelle direction vos données ont tendance à se déplacer, utilisez un test unilatéral. Dans l`exemple donné, vous vous attendez à ce que les notes des élèves s`améliorent ; c`est pourquoi vous utilisez un test unilatéral. 
Les chercheurs réalisent généralement une petite étude pilote pour éclairer leur analyse de la force et déterminer la taille de l`échantillon nécessaire pour une étude plus vaste et plus complète. Si vous n`avez pas les ressources nécessaires pour faire une étude pilote complexe, faites des estimations sur les moyennes possibles en vous basant sur la lecture de la littérature et des études que d`autres personnes ont pu faire. Cela vous donnera un bon point de départ pour la taille de l`échantillon pour commencer. 

Par exemple, pour trouver la note moyenne du groupe qui a lu le matériel avant le cours, regardons quelques données. Pour simplifier, nous utilisons un jeu de données de 5 points : 90, 91, 85, 83 et 94. Additionnez toutes les données : 90 + 91 + 85 + 83 + 94 = 443. Divisez la somme par le nombre de données, N = 5:443 / 5 = 88.6. La note moyenne de ce groupe est de 88,6. 
(90 à 88,6), (91 à 88,6), (85 à 88,6), (83 à 88,6) et (94 à 88,6). Les nombres calculés sont maintenant 1,4, 2,4, -3,6, -5,6 et 5,4. 
Dans notre exemple, nous travaillons maintenant avec 1,96 5,76, 12,96, 31,36 et 29,16. L`addition de ces carrés donne : 1,96 + 5,76 + 12,96 + 31,36 + 29,16 = 81,2. 
Soustraire : N – 1 = 5 – 1 = 4 Pièce : 81,2/4 = 20,3 
Dans notre exemple, l`écart type des notes finales des étudiants qui ont lu le matériel avant le cours est : s = 20,3 = 4,51. 

µ1 est la moyenne du premier groupe. µ2 est la moyenne du deuxième groupe. sré est la variance entre les échantillons. Utiliser la plus grande moyenne comme µ1, donc vous n`avez pas de valeur négative pour t. Dans notre exemple, disons que la moyenne de l`échantillon pour le groupe 2 (ceux qui n`ont pas lu) était de 80. Le t-score est alors : t = (µ1 – µ2)/sré = (88,6 – 80)/3,29 = 2,61. 

avec 8 jours.F. et un t-score de 2,61, la valeur p pour un test unilatéral se situe entre 0,01 et 0,025. Parce que notre niveau de signification défini est inférieur ou égal à 0,05, nos données sont statistiquement significatives. Avec ces données, nous rejetons l`hypothèse nulle et acceptons l`hypothèse alternative : les élèves qui lisent le matériel avant le cours obtiennent de meilleures notes finales. 
Évaluer l'importance statistique
Teneur
Le test d`hypothèse est soutenu par une analyse statistique. La signification statistique est calculée à partir d`une valeur p, qui indique la probabilité du résultat observé, étant donné qu`un certain énoncé (l`hypothèse nulle) est satisfait. Si cette valeur p est inférieure au niveau de signification indiqué (généralement 0,05), alors l`expérimentateur peut supposer que l`hypothèse nulle est fausse et accepter l`hypothèse alternative. À l`aide d`un simple test t, vous pouvez calculer une valeur p et comparer la signification entre deux groupes différents d`un ensemble de données.
Pas
Partie 1 sur 3 : Configuration de votre expérience

1. Définissez votre hypothèse. La première étape de l`évaluation de la signification statistique consiste à définir la question à laquelle il faut répondre et à poser votre hypothèse. L`hypothèse est une déclaration sur vos données expérimentales et les différences qui peuvent exister dans la population. Dans chaque expérience, il y a à la fois une hypothèse nulle et une hypothèse alternative. En général, vous comparerez deux groupes pour voir s`ils sont identiques ou différents.
- L`hypothèse nulle (H0) indique généralement qu`il n`y a pas de différence entre vos deux ensembles de données. Par exemple : les étudiants qui ont lu le matériel avant le cours n`obtiennent pas de meilleures notes finales.
- L`hypothèse alternative (Hune) est le contraire de l`hypothèse nulle et est l`affirmation que vous essayez de soutenir avec vos données expérimentales. Par exemple : les élèves qui ont lu le matériel avant le cours obtiennent de meilleures notes finales.

2. Définissez le niveau de signification pour déterminer à quel point vos données doivent être inhabituelles avant de pouvoir être considérées comme importantes. Le niveau de signification (également appelé alpha) est le seuil que vous définissez pour déterminer la signification. Si la valeur p est inférieure ou égale au seuil de signification défini, les données peuvent être considérées comme statistiquement significatives.

3. Décider d`utiliser un test unilatéral ou bilatéral. L`une des hypothèses émises par un test t est que les données sont normalement distribuées. Une distribution normale des données forme une courbe en cloche avec la plupart des données de test tombant au milieu. Le test t est un test mathématique pour voir si les données tombent en dehors de la distribution normale (au-dessus ou en dessous), dans les "queues" de la courbe.

4. Déterminer la taille de l`échantillon avec une analyse de force. La puissance d`un test est la probabilité que le résultat attendu soit observé, compte tenu d`une taille d`échantillon spécifique. Le seuil commun de force (ou ) est de 80%. Une analyse de puissance peut devenir un peu délicate sans quelques données préliminaires car vous avez besoin d`informations sur les valeurs moyennes attendues entre chaque groupe et leurs écarts types. Utilisez un calculateur d`analyse de force en ligne pour déterminer la taille d`échantillon optimale pour vos données.
Partie 2 sur 3: Calcul de l`écart type

1. Trouver la formule de l`écart type. L`écart type est une mesure de la diffusion de vos données. Il vous donne des informations sur la similitude de chaque point de données dans votre échantillon. À première vue, l`équation peut sembler un peu compliquée, mais les étapes suivantes vous guideront tout au long du calcul. La formule est : s = ((xje – µ)/(N – 1)).
- s est l`écart type.
- ∑ indique que vous devez additionner toutes les valeurs d`échantillon collectées.
- Xje représente chaque valeur individuelle de vos données.
- µ est la moyenne (ou centre) de vos données pour chaque groupe.
- N est le total de l`échantillon.

2. Faire la moyenne des données de test dans chaque groupe. Pour calculer l`écart type, vous devez d`abord faire la moyenne des données de test dans les groupes individuels. La moyenne est désignée par la lettre grecque mu ou µ. Pour ce faire, additionnez chaque donnée, puis divisez-la par le nombre total de données.

3. Soustraire chaque métrique de la moyenne. La partie suivante du calcul comprend la partie (xje – µ) de l`équation. Vous soustrayez chaque donnée de la moyenne qui vient d`être calculée. Dans notre exemple, vous vous retrouvez avec cinq soustractions.

4. Carré chacun de ces nombres et additionnez-les. Chacun des nouveaux nombres que vous venez de calculer sera maintenant au carré. Cette étape crée également des signes négatifs. Si vous avez un signe moins après cette étape ou à la fin de votre calcul, vous avez peut-être oublié cette étape.

5. Divisez ceci par la taille de l`échantillon total, moins 1. La formule divise par N-1, car elle corrige le fait que vous n`avez pas encore compté une population entière ; vous prenez un échantillon de la population de tous les élèves pour faire une estimation.

6. Prendre la racine carrée. Une fois que vous avez divisé par le nombre de données moins un, calculez la racine carrée de ce dernier nombre. C`est la dernière étape du calcul de l`écart type. Il existe des programmes statistiques qui peuvent faire ce calcul pour vous, après avoir entré les données brutes.
Partie 3 sur 3: Déterminer l`importance

1. Calculez la différence entre vos deux groupes de l`échantillon. Jusqu`à présent, l`exemple n`a couvert qu`un des groupes d`échantillons. Si vous souhaitez comparer deux groupes, vous aurez bien entendu les données des deux groupes. Calculez l`écart type du deuxième groupe de données de test et utilisez-le pour calculer la différence entre les deux groupes expérimentaux. La formule de la variance est sré = ((s1/N1) + (s2/N2)).
- sré est la variance entre vos groupes.
- s1 est l`écart type du groupe 1, et N1 est la taille de l`échantillon du groupe 1.
- s2 est l`écart type du groupe 2, et N2 est la taille de l`échantillon du groupe 2.
- Pour les besoins de notre exemple, disons que les données du groupe 2 (étudiants qui n`avaient pas lu avant le cours) avaient une taille d`échantillon de 5 et un écart type de 5,81. L`écart est :
- sré = ((s1)/N1) + ((s2)/N2))
- sré = (((4,51)/5) + ((5,81)/5)) = √((20,34/5) + (33,76/5)) = (4,07 + 6,75) = √10,82 = 3,29.

2. Calculez le t-score de vos données. Avec un t-score, vous pouvez convertir les données sous une forme que vous pouvez comparer avec d`autres données. Avec les scores t, vous pouvez effectuer un test t pour calculer la probabilité que deux groupes diffèrent significativement l`un de l`autre. La formule pour un t-score est : t = (µ1 – µ2)/sré.

3. Déterminez le degré de liberté de votre échantillon. Lors de l`utilisation du score t, les degrés de liberté sont déterminés à l`aide de la taille de l`échantillon. Additionnez le nombre de données de test de chaque groupe, puis divisez par deux. Dans notre exemple, les degrés de liberté ; d.F.) 8, car il y avait cinq données dans le premier groupe et cinq dans le deuxième groupe ((5 + 5) – 2 = 8).

4. Utiliser une table t pour évaluer l`importance. Un tableau avec les scores t et le nombre de degrés de liberté peut être trouvé dans un livre de statistiques standard ou en ligne. Regardez la rangée de degrés de liberté pour vos données et trouvez la valeur p qui correspond à votre t-score.

5. Envisagez une étude de suivi. De nombreux chercheurs font une petite étude pilote avec quelques mesures pour comprendre comment mettre en place une étude plus large. Une autre étude, avec plus de mesures, vous aidera à augmenter votre confiance dans votre conclusion.
Des astuces
- La statistique est un domaine vaste et compliqué. Suivez un cours du secondaire ou de l`enseignement supérieur sur l`inférence statistique pour mieux comprendre la signification statistique.
Mises en garde
- Cette analyse est spécifique à un test t pour tester les différences entre deux populations normalement distribuées. Vous pouvez avoir besoin d`un test statistique différent selon la complexité de votre collecte de données.
Articles sur le sujet "Évaluer l'importance statistique"
Оцените, пожалуйста статью
Similaire
Populaire