La plupart des gens connaissent le concept d`intérêt, mais tout le monde ne sait pas comment le calculer. L`intérêt est la valeur ajoutée à un prêt ou à une avance pour payer l`utilisation de l`argent d`autrui sur une période de temps. Les intérêts peuvent être calculés de trois manières. L`intérêt ordinaire est le plus facile à calculer et s`applique généralement aux prêts à court terme. L`intérêt composé est un peu plus compliqué et vaut plus. Après tout, la composition constante des intérêts augmentera le plus rapidement et c`est la formule que la plupart des banques utilisent pour les prêts hypothécaires. Les informations dont vous avez besoin pour tous ces calculs sont généralement les mêmes, mais le calcul est un peu différent pour chacun.
Pas
Méthode 1 sur 3 : Calcul de l`intérêt simple
1.
Déterminer le montant principal. Le principal est le montant d`argent que vous utiliserez pour calculer les intérêts. Il peut s`agir d`un montant que vous déposez sur un compte d`épargne ou investissez dans une sorte d`investissement. Dans ce cas, vous pouvez calculer les intérêts que vous gagnez. L`alternative est que si vous empruntez de l`argent, comme pour une hypothèque, le capital est le montant que vous empruntez, et vous pouvez calculer les intérêts que vous devez.
- Dans les deux cas, que vous alliez percevoir ou payer des intérêts, le montant du principal est généralement symbolisé par la variable P.
- Par exemple, si vous avez emprunté 2 000 $ à un ami, ces 2 000 $ sont le capital.
2. Déterminer l`intérêt. Avant de pouvoir calculer la valeur du capital qui augmentera, vous devez connaître le taux d`intérêt auquel le capital augmentera. C`est votre intérêt. L`intérêt est généralement annoncé ou convenu entre les parties avant que le prêt ne soit consenti.
Par exemple, supposons que vous ayez prêté de l`argent à un ami en vertu d`un accord selon lequel, après six mois, il remboursera les 2 000 $ avec un intérêt de 1,5%. L`intérêt unique est de 1,5%. Mais avant de pouvoir utiliser le pourcentage de 1,5%, vous devez le convertir en nombre décimal. Pour convertir le pourcentage en décimal, divisez le pourcentage par 100 :1,5% 100=0,015.3. Vérifier la durée du prêt. Le terme est un autre nom pour la durée du prêt. Dans certains cas, vous acceptez la durée du prêt en empruntant le montant. Par exemple : la plupart des hypothèques ont une durée fixe. Dans de nombreux cas, avec un prêt privé, l`emprunteur et le prêteur s`entendent sur une durée convenue à l`avance.
Il est important que la durée du terme corresponde au taux d`intérêt, ou au moins soit mesurée dans les mêmes unités. Par exemple : s`il s`agit d`un taux d`intérêt annuel, alors votre terme doit également être mesuré en années. Si le taux annoncé est de 3 % par an, mais que le prêt n`est valable que pour six mois, vous calculez alors un taux d`intérêt annuel de 3 % sur une période de 0,5 an.Autre exemple : si le taux convenu est de 1% par mois, et que vous empruntez l`argent pendant six mois, la durée du calcul est de six mois.4. Calculer les intérêts. Pour calculer les intérêts, multipliez le principal par le taux d`intérêt et la durée du prêt. Cette formule peut être exprimée algébriquement par :
 En utilisant l`exemple de prêt à un ami ci-dessus, le principal (
En utilisant l`exemple de prêt à un ami ci-dessus, le principal ( ) égal à 2 000 $ et le pourcentage (
) égal à 2 000 $ et le pourcentage ( ) est de 0,015 sur une période de six mois. Étant donné que l`accord dans cet exemple était d`une durée de six mois, la variable
) est de 0,015 sur une période de six mois. Étant donné que l`accord dans cet exemple était d`une durée de six mois, la variable  dans ce cas 1. Calculez ensuite les intérêts comme suit :
dans ce cas 1. Calculez ensuite les intérêts comme suit : . Ainsi les intérêts dus sont de 30 €.Si vous voulez calculer le montant total dû (A) avec les intérêts et le produit du capital, vous utilisez la formule
. Ainsi les intérêts dus sont de 30 €.Si vous voulez calculer le montant total dû (A) avec les intérêts et le produit du capital, vous utilisez la formule  . Ce calcul ressemble à ceci :
. Ce calcul ressemble à ceci :



5. Essayez un autre exemple. Supposons que vous déposez 5 000 $ dans un compte d`épargne avec un intérêt annuel de 3 %. Après seulement trois mois, vous retirez l`argent, ainsi que les intérêts.



 En trois mois vous gagneriez 37,50 € d`intérêts.Notez que t=0,25, car trois mois est un quart (0,25) de la période d`origine d`un an.
En trois mois vous gagneriez 37,50 € d`intérêts.Notez que t=0,25, car trois mois est un quart (0,25) de la période d`origine d`un an.Méthode 2 sur 3 : Calculer l`intérêt composé
1.
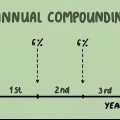
Comprendre ce qu`est l`intérêt composé. Les intérêts composés signifient que lorsque vous gagnez des intérêts, les intérêts sont ajoutés au montant de votre compte et vous commencez à gagner (ou à payer) des intérêts en plus des intérêts. Un exemple simple : si vous déposez 100 $ à 5% d`intérêt par an, vous aurez gagné 5 $ d`intérêt à la fin d`une année. Si vous remettez cela sur votre compte, à la fin de la deuxième année, vous aurez gagné 5 % de 105 $, pas seulement les 100 $ d`origine. Au fil du temps, cela peut augmenter de manière très significative.
- La formule de calcul de la valeur (A) des intérêts composés est la suivante :

2.
Savoir ce que signifie le principal. Comme pour les intérêts simples, le calcul commence par le montant du principal. Le calcul est le même que vous calculiez les intérêts sur l`argent emprunté ou prêté. Le principal est généralement désigné par la variable

.
3.
Déterminer le pourcentage. Le taux d`intérêt doit être convenu avant le prêt et affiché sous forme de nombre décimal pour le calcul. Sachez que le pourcentage peut être converti en un nombre décimal en le divisant par 100 (ou plus vite, en déplaçant la décimale de deux positions vers la gauche). Assurez-vous de savoir pour quelle période le taux d`intérêt s`applique. Le pourcentage a

comme symbole.
4. Savoir quand l`intérêt est composé. Les intérêts composés signifient que les intérêts sont calculés périodiquement et ajoutés au montant principal. Pour certains prêts, cela peut arriver une fois par an. Pour d`autres, c`est tous les mois ou tous les trimestres. Vous devez savoir à quelle fréquence les intérêts seront composés par an.
Si les intérêts sont composés annuellement, alors n=1.Si les intérêts sont composés trimestriellement, alors argent n=4.5. Connaître la durée du prêt. Le terme est la période sur laquelle les intérêts seront calculés. La durée est généralement exprimée en années. Si vous devez calculer les intérêts sur une période différente, vous devez les convertir en années.
Par exemple : avec un prêt d`un an,  . Cependant, avec une durée de 18 mois,
. Cependant, avec une durée de 18 mois,  .
.6. Déterminer les variables de la situation. Dans cet exemple, supposons que vous déposez 5 000 $ sur un compte d`épargne avec un intérêt mensuel composé de 5 %. Quelle est la valeur de ce compte après trois ans?
Déterminez d`abord les variables dont vous avez besoin pour résoudre le problème. Dans ce cas:



sept. Appliquer la formule et calculer l`intérêt composé. Une fois que vous avez compris ce qui doit être fait et quelles variables sont nécessaires, appliquez-les à la formule pour calculer le taux d`intérêt.
Dans le problème ci-dessus, cela ressemble à ceci:




 Ainsi, après trois ans d`intérêts composés, vous disposez d`un montant de 808 €, en plus des 5000 € initialement déposés.
Ainsi, après trois ans d`intérêts composés, vous disposez d`un montant de 808 €, en plus des 5000 € initialement déposés.Méthode 3 sur 3 : Calculer les intérêts composés récurrents
1.
Comprendre ce qu`est l`intérêt composé renouvelable. Comme vous l`avez vu dans l`exemple précédent, les intérêts composés augmentent plus rapidement que les intérêts simples en ajoutant des intérêts au capital à certains moments. La compilation trimestrielle a plus de valeur qu`annuelle. Compiler mensuellement est encore plus précieux qu`annuellement. La situation la plus rentable serait lorsque l`intérêt est composé en permanence, c`est-à-dire à chaque instant. Dès que les intérêts peuvent être calculés, ils sont ajoutés au compte et ajoutés au capital. Ceci n`est bien entendu qu`un cas théorique.
- En utilisant un peu de mathématiques, les mathématiciens ont développé une formule pour simuler les intérêts qui sont continuellement composés et ajoutés au compte. Cette formule, utilisée pour calculer les intérêts composés renouvelables, est la suivante :


2. Connaître les variables de calcul des intérêts. La formule des intérêts composés renouvelables est très similaire aux situations précédentes, mais avec quelques ajustements mineurs. Les variables de la formule sont :
 est la valeur future (ou le montant) d`argent que vaudra le prêt après avoir composé les intérêts.
est la valeur future (ou le montant) d`argent que vaudra le prêt après avoir composé les intérêts. est le principal.La constante
est le principal.La constante  . Bien que cela ressemble à une variable, il s`agit en fait d`une constante. La lettre
. Bien que cela ressemble à une variable, il s`agit en fait d`une constante. La lettre  est un nombre spécial appelé « constante d`Euler », d`après le mathématicien Leonard Euler qui a découvert ses propriétés.La plupart des calculatrices graphiques avancées ont un bouton pour
est un nombre spécial appelé « constante d`Euler », d`après le mathématicien Leonard Euler qui a découvert ses propriétés.La plupart des calculatrices graphiques avancées ont un bouton pour  . Si vous appuyez sur ce bouton, avec le chiffre 1, ainsi
. Si vous appuyez sur ce bouton, avec le chiffre 1, ainsi  , alors vous voyez que la valeur de
, alors vous voyez que la valeur de  est d`environ 2,718.
est d`environ 2,718. est l`intérêt par an.
est l`intérêt par an. est la durée du prêt, en années.
est la durée du prêt, en années.3. Connaître les détails de votre prêt. Les banques utilisent généralement des intérêts composés renouvelables pour les hypothèques. Supposons que vous ayez 200 €.000 veulent emprunter à un taux d`intérêt de 4,2 % pour un prêt hypothécaire de 30 ans. Les variables que vous utiliserez pour ce calcul sont donc :

 , encore une fois, pas une variable mais la constante 2,718.
, encore une fois, pas une variable mais la constante 2,718.

4. Utiliser la formule de calcul des intérêts. Appliquez les valeurs à la formule pour calculer le montant des intérêts que vous devrez payer sur le prêt sur 30 ans.




 Notez l`énorme valeur des intérêts composés renouvelables.
Notez l`énorme valeur des intérêts composés renouvelables. Articles sur le sujet "Calculer les intérêts"





 ) égal à 2 000 $ et le pourcentage (
) égal à 2 000 $ et le pourcentage ( ) est de 0,015 sur une période de six mois. Étant donné que l`accord dans cet exemple était d`une durée de six mois, la variable
) est de 0,015 sur une période de six mois. Étant donné que l`accord dans cet exemple était d`une durée de six mois, la variable  dans ce cas 1. Calculez ensuite les intérêts comme suit :
dans ce cas 1. Calculez ensuite les intérêts comme suit : . Ainsi les intérêts dus sont de 30 €.
. Ainsi les intérêts dus sont de 30 €. . Ce calcul ressemble à ceci :
. Ce calcul ressemble à ceci :










 .
.
 comme symbole.
comme symbole.

 . Cependant, avec une durée de 18 mois,
. Cependant, avec une durée de 18 mois,  .
.













 est la valeur future (ou le montant) d`argent que vaudra le prêt après avoir composé les intérêts.
est la valeur future (ou le montant) d`argent que vaudra le prêt après avoir composé les intérêts. est le principal.
est le principal. . Bien que cela ressemble à une variable, il s`agit en fait d`une constante. La lettre
. Bien que cela ressemble à une variable, il s`agit en fait d`une constante. La lettre  est un nombre spécial appelé « constante d`Euler », d`après le mathématicien Leonard Euler qui a découvert ses propriétés.
est un nombre spécial appelé « constante d`Euler », d`après le mathématicien Leonard Euler qui a découvert ses propriétés. . Si vous appuyez sur ce bouton, avec le chiffre 1, ainsi
. Si vous appuyez sur ce bouton, avec le chiffre 1, ainsi  , alors vous voyez que la valeur de
, alors vous voyez que la valeur de  est d`environ 2,718.
est d`environ 2,718. est l`intérêt par an.
est l`intérêt par an. est la durée du prêt, en années.
est la durée du prêt, en années.

 , encore une fois, pas une variable mais la constante 2,718.
, encore une fois, pas une variable mais la constante 2,718.