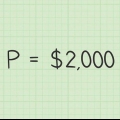Comment calculer l'intérêt composé: 15 étapes (avec photos)

Teneur

Pas
Des astuces

L`intérêt composé diffère de l`intérêt simple en ce que le rendement des intérêts est calculé à la fois sur l`investissement initial (principal) et sur les intérêts courus à ce jour, plutôt que simplement sur le principal. C`est pourquoi les comptes à intérêt composé croissent plus rapidement que les comptes à intérêt simple. De plus, la valeur augmentera encore plus rapidement si les intérêts sont composés plusieurs fois par an. Les intérêts composés (également appelés intérêts) peuvent être trouvés avec divers produits d`investissement et également sous forme d`intérêts sur certains types de prêts, tels que les dettes de carte de crédit. Avec les bonnes équations, calculer de combien un montant augmentera grâce aux intérêts composés est très simple.

Pas

Partie 1 sur 3: Calcul de l`intérêt composé annuel

Image intitulée Calculer l`intérêt composé Étape 1

1. Définir les intérêts composés annuels. Le taux d`intérêt indiqué sur votre prospectus d`investissement ou votre contrat de prêt est annuel. Si vous contractez un crédit auto à 6% d`intérêt par exemple, vous payez 6% d`intérêt par an. Un intérêt composé de fin d`année est le calcul d`intérêt composé le plus simple.

Les intérêts composés sur une dette peuvent être calculés annuellement, mensuellement ou même quotidiennement.
Plus votre dette est aggravée, plus vos intérêts s`accumuleront rapidement.
Vous pouvez considérer les intérêts composés du point de vue d`un investisseur ou d`un débiteur. Les intérêts composés fréquemment calculés signifient que les revenus d`intérêts des investisseurs augmenteront plus rapidement. Cela signifie également que le débiteur devra plus d`intérêts sur une dette en cours.
Par exemple, les intérêts peuvent être calculés annuellement sur un compte d`épargne, tandis que les intérêts d`un prêt flash peuvent être calculés mensuellement voire hebdomadairement.

Image intitulée Calculer l`intérêt composé Étape 2

2. Calculer l`intérêt annuel composé pour l`année 1. Supposons que vous possédiez une obligation d`État à 1 €.000, à un taux d`intérêt de 6%. Les obligations d`État versent des dividendes chaque année en fonction des intérêts et de la valeur actuelle.

L`intérêt pour l`année 1 sera alors de 60 € (1 €.000 x 6%).

Pour calculer les intérêts pour l`année 2, vous devez ajouter le capital initial au total des intérêts à ce jour. Dans ce cas, le principal de l`année 2 est égal à 1 €.060 (1 €.000 + 60 €). La valeur de l`obligation est donc de 1 €.060 et les intérêts à payer sont calculés sur cette valeur.

Image intitulée Calculer l`intérêt composé Étape 3

3. Calculer l`intérêt composé pour les années suivantes. Pour voir l`impact plus important des intérêts composés, calculez les intérêts des années suivantes. Le principal continue de croître d`année en année.

Multipliez le capital de l`année 2 par le taux d`intérêt de l`obligation (1 $.060 X 6% = 63,60 €). L`intérêt obtenu est supérieur de 3,60 € (63,60 € - 60,00 €). C`est parce que le capital est passé de 1 $.000 à 1 €.060.

Pour l`année 3, le principal est de 1 €.123,60 (1 €.060 + 63,60 €). L`intérêt pour l`année 3 est de 67,42 €. Ce montant est ajouté au capital pour le calcul de l`année 4.

Plus une dette est impayée, plus l`impact des intérêts composés est important. En souffrance signifie que la dette doit encore être payée par le débiteur.

Sans intérêts composés, les intérêts gagnés sur l`année 2 seraient de 60 $ (1 €.000 X 6%). En fait, chaque année, l`intérêt serait de 60 $ si vous obteniez des intérêts composés. C`est ce qu`on appelle l`intérêt simple.

Image intitulée Calculer l`intérêt composé Étape 4

4. Créer un document Excel pour calculer les intérêts composés. Il peut être utile de visualiser les intérêts composés en créant un modèle Excel simple de la croissance de votre investissement. Commencez par ouvrir un document et étiquetez la cellule supérieure dans les colonnes A, B et C comme « Année », « Valeur » et « Intérêts gagnés » respectivement.

Tapez les années (0-5) dans les cellules A2 à A7.

Tapez le principal dans la cellule B2. Supposons que vous ayez commencé avec 1 €.000. Type 1000.

Dans la cellule B3, tapez `= B2 *1,06` et appuyez sur Entrée. Cela signifie que votre intérêt est composé annuellement à un intérêt de 6% (0,06). Cliquez sur le coin inférieur droit de la cellule B3 et faites glisser la formule vers la cellule B7. Les nombres sont maintenant remplis correctement.

Placez un 0 dans la cellule C2. Dans la cellule C3, tapez `=B3-B2` et appuyez sur Entrée. Cela donne la différence entre les valeurs dans les cellules B3 et B2, ce qui représente l`intérêt. Cliquez sur le coin inférieur droit de la cellule C3 et faites glisser la formule vers la cellule C7. Les valeurs doivent être renseignées automatiquement.

Répétez cette procédure pendant autant d`années que vous le souhaitez. Vous pouvez également modifier facilement les valeurs du principal et des taux d`intérêt en modifiant les formules utilisées et le contenu des cellules.

Partie 2 sur 3: Calcul des intérêts composés sur les investissements

Image intitulée Calculer l`intérêt composé Étape 5

1. Apprenez la formule des intérêts composés. La formule des intérêts composés calcule la valeur future de l`investissement après un certain nombre d`années. La formule elle-même est la suivante :

F V = p (1 + \frac{je}{c})^{m * c}

$FV=P(1+{frac{i}{c}})^{{n*c}}$ Les variables dans l`équation sont définies comme suit :

`FV` est la valeur future. C`est le résultat du calcul.
`P` est votre principal.
`i` est le taux d`intérêt annuel.
« c » est le taux d`intérêt composé (à quelle fréquence les intérêts composés sont calculés annuellement).
`n` est le nombre d`années à calculer.

Image intitulée Calculer l`intérêt composé Étape 6

2. Collecter les variables pour la formule des intérêts composés. Si les intérêts sont calculés plus souvent qu`une fois par an, il est difficile de calculer la formule manuellement. Vous pouvez utiliser une formule d`intérêt composé pour tout calcul. Pour utiliser la formule, vous avez besoin des informations suivantes :

Déterminer le montant principal de l`investissement. Il s`agit du montant initial de votre investissement. Il peut s`agir du montant que vous avez déposé sur votre compte ou du prix initial de l`obligation. Par exemple, supposons que votre capital dans un compte d`investissement soit de 5 €.000 est.

Trouver le taux d`intérêt de l`investissement. Le taux d`intérêt doit être un montant annuel, exprimé en pourcentage du montant principal. Par exemple, un taux d`intérêt de 3,45 % sur le principal de 5 €.000.

Lors du calcul, le taux d`intérêt doit être saisi sous forme décimale. Convertissez-le en divisant le taux d`intérêt par 100. Dans cet exemple, il devient 3,45/100 = 0,0345.

Vous devez également savoir à quelle fréquence les intérêts sont composés. Les intérêts sont généralement composés annuellement, mensuellement ou quotidiennement. Supposons, par exemple, qu`il s`agisse d`intérêts mensuels. Cela signifie que votre taux d`intérêt (`c`) doit être saisi comme 12.

Déterminez sur quelle période vous voulez calculer. Cela pourrait être un objectif annuel de croissance, comme 5 ou 10 ans, ou la maturité de l`obligation. La date d`échéance d`une obligation est la date à laquelle le capital de l`investissement doit être remboursé. À titre d`exemple, nous utilisons deux ans ici, alors entrez un 2.

Image intitulée Calculer l`intérêt composé Étape 7

3. Utilisez la formule. Remplacez vos variables aux bons endroits. Veuillez vérifier pour vous assurer que vous les avez entrés correctement. En particulier, assurez-vous que les intérêts sont saisis sous forme décimale et que vous avez utilisé la valeur correcte pour `c` (taux d`intérêt).

L`exemple d`investissement est alors saisi comme suit :

F V = 5000 (1 + 0, 0345 12)^{2 * 12}

$FV=5000(1+{frac{0.0345}{12}})^{{2*12}}$

Calculer l`exposant et la partie de la formule entre parenthèses séparément. Il s`agit d`un concept des mathématiques appelé « ordre des opérations ». Vous pouvez lire des articles sur l`ordre des opérations sur wikiHow.

Image intitulée Calculer l`intérêt composé Étape 8

4. Complétez les calculs mathématiques dans la formule. Simplifiez le problème en résolvant d`abord les termes entre parenthèses, en commençant par la fraction.

Calculez d`abord la fraction entre parenthèses. Le résultat:

F V = 5000 (1 + 0, 00288) 2 * 12

$FV=5000(1+0.00288)^{{2*12}}$

Ajouter des nombres entre parenthèses ensemble. Le résultat:

F V = 5000 (1, 00288) 2 * 12

$FV=5000(1.00288)^{{2*12}}$

Résoudre la multiplication dans l`exposant (la dernière partie au-dessus de la parenthèse fermante). Le résultat devrait ressembler à ceci :

F V = 5000 (1, 00288) 24

$FV=5000(1.00288)^{{24}}$

Augmenter le nombre entre parenthèses à la puissance de l`exposant. Cela peut être fait sur une calculatrice en entrant d`abord la valeur entre parenthèses (1.00288 dans l`exemple), en appuyant sur le bouton

X oui

$x^{y}$ , puis entrez l`exposant (24 dans ce cas), après quoi vous appuyez sur Entrée. Le résultat de cet exemple est

F V = 5000 (1, 0715)

$VF=5000(1.0715)$ .

Enfin, multipliez le principal par le nombre entre parenthèses. Le résultat dans l`exemple est de 5 €.000 x 1,0715 = 5 €.357,50. C`est le solde du compte à la fin de la deuxième année.

Image intitulée Calculer l`intérêt composé Étape 9

5. Soustraire le principal de votre réponse. Cela renvoie le montant des intérêts.

Soustraire le principal de 5 €.000 à partir de la valeur future de 5 €.357,50 et vous obtenez 5 €.375,50 - 5 €.000 = 357,50 €

Vous avez gagné 357,50 € d`intérêts après deux ans.

Partie 3 sur 3: Calcul des intérêts composés avec versements réguliers

Image intitulée Calculer l`intérêt composé Étape 10

1. Apprendre la formule. Les calculs d`intérêts composés peuvent augmenter encore plus rapidement si vous effectuez des dépôts réguliers, tels que le transfert d`un montant mensuel sur un compte d`épargne. La formule est plus longue que celle utilisée pour calculer les intérêts composés sans versements réguliers, mais suit les mêmes principes. La formule est la suivante :

F V = p (1 + \frac{je}{c})^{m * c} + R ((1 + \frac{je}{c})^{m * c} - 1) \frac{je}{c}

$FV=P(1+{frac{i}{c}})^{{n*c}}+{frac{R((1+{frac{i}{c}})^{{n *c}}-1)}{{frac{i}{c}}}}$ Les variables de l`équation sont également les mêmes que dans l`équation précédente, avec un ajout :

`P` est le principal.
`i` est le taux d`intérêt annuel.
« c » est la fréquence des taux d`intérêt et représente le nombre de fois que les intérêts sont composés annuellement.
`n` est le nombre d`années.
`R` est le montant de la cotisation mensuelle.

Image intitulée Calculer l`intérêt composé Étape 11

2. Remplissez les variables. Pour calculer la valeur future de ce type de compte, vous avez besoin du capital (ou valeur actuelle) du compte, du taux d`intérêt annuel, de la fréquence des intérêts, du nombre d`années à calculer et du montant de votre cotisation mensuelle. Cette information devrait être dans votre accord d`investissement.

Assurez-vous de convertir le taux d`intérêt annuel en un nombre décimal. Pour ce faire, divisez le pourcentage par 100. Par exemple, en supposant le taux d`intérêt ci-dessus de 3,45%, nous divisons 3,45 par 100 et vous obtenez 0,0345.

Pour la fréquence d`intérêt, vous utilisez le nombre de fois par an que l`intérêt est calculé. Cela signifie annuel numéro 1, mensuel 12 et quotidien 365 (ne vous inquiétez pas des années bissextiles).

Image intitulée Calculer l`intérêt composé Étape 12

3. Remplissez les variables. On continue avec l`exemple ci-dessus : supposons que vous décidiez de virer 100€ par mois sur votre compte. A propos de ce compte, avec un capital de 5€.000, l`intérêt composé est calculé mensuellement avec un taux d`intérêt annuel de 3,45 %. Nous allons calculer la croissance du compte sur deux ans.

La formule finale utilisant ces informations est la suivante :

F V = 5000 (1 + 0, 0345 12)^{2 * 12} + 100 ((1 + 0, 0345 12)^{2 * 12} - 1) \frac{0, 0345}{12}

$FV=5000(1+{frac{0.0345}{12}})^{{2*12}}+{frac{100((1+{frac{0.0345}{12}}) ^{{2 *12}}-1)}{{frac{0.0345}{12}}}}$

Image intitulée Calculer l`intérêt composé Étape 13

4. Résous l`équation. Encore une fois, n`oubliez pas le bon ordre des opérations. Cela signifie que vous commencez par calculer les valeurs entre parenthèses.

Résolvez d`abord les fractions entre parenthèses. Cela signifie diviser `i` par `c` à trois endroits, le tout pour le même résultat de 0,00288. Maintenant, l`équation ressemble à ceci :

F V = 5000 (1 + 0, 00288) 2 * 12 + 100 ((1 + 0, 00288) 2 * 12 - 1) 0, 00288

$FV=5000(1+0.00288)^{{2*12}}+{frac{100((1+0.00288)^{{2*12}}-1)}{0.00288}}$

Résoudre l`addition entre parenthèses. Cela signifie que vous ajoutez le 1 au résultat de la partie précédente. Ainsi:

F V = 5000 (1, 00288) 2 * 12 + 100 ((1, 00288) 2 * 12 - 1) 0, 00288

$FV=5000(1.00288)^{{2*12}}+{frac{100((1.00288)^{{2*12}}-1)}{0.00288}}$

Résoudre la multiplication dans les exposants. Cela signifie multiplier les deux nombres qui sont plus petits et au-dessus des parenthèses fermantes. Dans l`exemple : 2 x 12 = 24. Ainsi:

F V = 5000 (1, 00288) 24 + 100 ((1, 00288) 24 - 1) 0, 00288

$FV=5000(1.00288)^{{24}}+{frac{100((1.00288)^{{24}}-1)}{0.00288}}$

Résoudre les exposants. Cela signifie augmenter le montant entre parenthèses avec le résultat de la dernière étape. Sur une calculatrice cela se fait en entrant la valeur entre parenthèses (1.00288 dans l`exemple), appuyez sur

X oui

$x^{y}$ et entrez la valeur de l`exposant (24). Ainsi:

F V = 5000 (1, 0715) + 100 (1, 0715 - 1) 0, 00288

$FV=5000(1.0715)+{frac{100(1,0715-1)}{0.00288}}$

soustraire. Soustraire 1 du résultat de la dernière étape dans la partie droite de l`équation (1,0715 - 1). Ainsi:

F V = 5000 (1, 0715) + 100 (0, 0715) 0, 00288

$FV=5000(1.0715)+{frac{100(0.0715)}{0.00288}}$

Multiplier. Cela signifie multiplier le principal par la valeur entre parenthèses et la contribution mensuelle par la même valeur entre parenthèses. Ainsi:

F V = 5357, 50 + sept, 15 0, 00288

$VF=5357.50+{frac{7.15}{0.00288}}$

Diviser la fraction. Ainsi:

F V = 5357, 50 + 2482, 64

$VF=5357,50+2482,64$

Additionner. Enfin, additionnez les deux nombres pour obtenir la valeur future du compte. Donc : 5€.357,50 + 2 €.482,64 = 7 €.840.14. Il s`agit de la valeur du compte après les deux ans.

Image intitulée Calculer l`intérêt composé Étape 14

5. Soustraire le principal et les paiements. Pour calculer les intérêts gagnés, vous devez soustraire le montant que vous avez déposé. Cela signifie additionner le principal, 5 €.000, à la valeur totale des sommes déposées, soit : 24 cotisations (2 ans x 12 mois/an) multipliées par les 100 € que vous avez déposés chaque mois, pour un total de 2400 €. Le total est de 5€.000 + 2 €.400 = 7400 €. Tirage 7€.400 sur la valeur future de 7 €.840,14, et vous avez le montant des intérêts, 440,14 €.

Image intitulée Calculer l`intérêt composé Étape 15

6. Développez votre calcul. Pour vraiment voir les avantages des intérêts composés, imaginez que vous continuez à déposer de l`argent sur le même compte chaque mois pendant 20 ans (au lieu de deux). Dans ce cas, la valeur future devient environ 45.000 dollars, alors que vous ne dépensez que 29 €.000, ce qui signifie que vos intérêts courus sont de 16 €.000 s`élève à.

Des astuces

Vous pouvez également calculer facilement les intérêts composés à l`aide d`un calculateur d`intérêts en ligne. Vous pouvez trouver un exemple sur le site du gouvernement américain : https://www.investisseur.gov/tools/calculators/compound-interest-calculator.
Un moyen rapide de déterminer l`intérêt composé est la "règle des 72". Commencez par diviser 72 par le montant des intérêts que vous obtenez, disons 4%. Donc dans ce cas 72/4 = 18. Ce résultat, 18, est approximativement le nombre d`années qu`il faudra pour doubler votre investissement au taux d`intérêt actuel. Gardez à l`esprit que la règle des 72 n`est qu`une approximation rapide, pas un résultat exact.
Vous pouvez également utiliser ces calculs pour faire des calculs « et si » qui peuvent vous dire combien vous gagnerez en fonction du taux d`intérêt, du capital, du taux d`intérêt ou du nombre d`années.