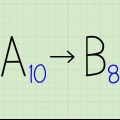Convertir binaire en octal : 11 étapes (avec photos)

Teneur

Pas
- Méthode 1 sur 2: Convertir à la main
- Méthode 2 sur 2: Conversions rapides et variantes
Des astuces

Les systèmes binaires et octaux sont deux systèmes de nombres différents couramment utilisés en informatique. Ils ont chacun une base différente - le binaire a la base 2 et l`octal a la base 8 - ce qui signifie qu`ils doivent être regroupés afin de convertir. Cependant, cela semble beaucoup plus compliqué que cette conversion très simple ne l`est en réalité.

Pas

Méthode 1 sur 2: Convertir à la main

Image intitulée Convertir le nombre binaire en nombre octal, étape 1

1. Reconnaître une plage de nombres binaires. Les nombres binaires sont simplement des séquences de uns et de zéros, tels que 101001, 001 ou même juste 1. Lorsque vous voyez une telle séquence de nombres, elle est généralement binaire. Cependant, certains livres et enseignants font également référence à des nombres binaires avec un indice « 2 », comme 1001₂, ceci pour éviter toute confusion avec le nombre décimal 1001.

Cet indice indique la `base` du nombre. Le binaire est un système de nombres en base deux et l`octal en base huit.

Image intitulée Convertir le nombre binaire en nombre octal, étape 2

2. Regrouper tous les uns et les zéros du binaire par groupes de trois, en partant de la droite. Il n`y a que deux chiffres binaires différents et huit chiffres octaux. Parce que

23 = 8,

$2^{3}=8,$ avez-vous besoin de trois nombres binaires pour représenter chaque nombre octal. Commencez à diviser en groupes sur la droite. Par exemple : le nombre binaire 101001 peut alors être divisé en 101 001.

Image intitulée Convertir le nombre binaire en nombre octal, étape 3

3. Ajoutez des zéros à gauche du dernier chiffre si vous n`avez pas assez de chiffres pour faire un groupe de trois chiffres. Le nombre binaire 10011011 a huit chiffres, pas un multiple de trois, mais toujours convertible en nombre octal. Ajoutez simplement des zéros supplémentaires au premier groupe jusqu`à ce qu`il ait trois places. Par exemple:

Original: 10011011

En groupes: 10 011 011

Après avoir ajouté des zéros : 010 011 011

Image intitulée Convertir le nombre binaire en nombre octal, étape 4

4. Ajoutez un 4, un 2 et un 1 à chaque chaîne de trois nombres pour indiquer les valeurs de position. Chacun des trois nombres binaires d`un ensemble représente une valeur de position particulière dans le système de nombres octaux. Le premier nombre est celui d`un 4, le second d`un 2, et le troisième a la valeur 1. Pour plus de clarté, écrivez ceci directement sous chaque chaîne de trois nombres binaires. Par exemple:

010 011 011
421 421 421

001
421

110 010 001
421 421 421

Remarque, si vous recherchez une méthode rapide, vous pouvez ignorer cette étape et comparer simplement la séquence de nombres binaires avec celle-ci .

Image intitulée Convertir le nombre binaire en nombre octal, étape 5

5. S`il y en a un au-dessus de l`une des valeurs de position, écrivez ce nombre (4, 2 ou 1) pour commencer la conversion. S`il y en a un au-dessus du "4" alors le nombre octal contient un 4. S`il y a un 0 au-dessus de la valeur de position 1, alors le nombre octal ne contient pas 1, alors mettez un espace, un zéro ou un tiret à cette place. Comme dans l`exemple suivant :

Problème:

Convertir 101010011₂ en octal.

Divisez-les en trois :

101 010 011

Ajoutez les valeurs de position :

101 010 011
421 421 421

Mettez en surbrillance chaque valeur de position :

101 010 011
421 421 421
401 020 021

Image intitulée Convertir le nombre binaire en nombre octal, étape 6

6. Additionnez les nouveaux nombres dans chaque groupe de trois chiffres. Si vous savez quelles valeurs de position sont dans le nombre octal, additionnez tous les chiffres par groupe. Donc, si vous avez 101, cela devient 4, 0 et 1, et cela donne 5 en conséquence (

4 + 0 + 1 = 5

$4+0+1=5$ ). Pour continuer avec l`exemple ci-dessus :

Problème:

Convertir 101010011₂ à un octal.

Séparez en trois, ajoutez des valeurs de lieu et marquez chaque lieu :

101 010 011
421 421 421
401 020 021

Additionnez chaque ensemble de trois :

$(4 + 0 + 1) (0 + 2 + 0) (0 + 2 + 1) = 5, 2, 3$ $(4+0+1)(0+2+0)(0+2+1)=5,2,3$

Image intitulée Convertir le nombre binaire en nombre octal, étape 7

sept. Placez les réponses nouvellement converties côte à côte pour former le nombre octal final. La division du nombre binaire était juste pour faciliter la conversion - le nombre d`origine était une longue chaîne. Alors, maintenant qu`il est converti, rassemblez le tout pour obtenir votre réponse finale. ce n`est pas plus.

Problème:

Convertir 101010011₂ en octal.

Divisez, ajoutez des valeurs de position, marquez des lieux et additionnez des totaux :

101 010 011
5 — 2—3

Replacez les nombres convertis les uns à côté des autres :

523

Image intitulée Convertir le nombre binaire en nombre octal, étape 8

8. Ajoutez un indice 8 (comme celui-ci ₈) pour terminer la conversion. Il n`y a fondamentalement aucun moyen de savoir si 523 fait référence à un nombre octal ou décimal, sans la notation correcte. Pour vous assurer que votre professeur sait que vous avez correctement résolu le problème, mettez un indice 8 à côté de votre réponse, en faisant référence à un nombre octal (base 8).

Problème:

Convertir 101010011₂ en octal.

Conversion:

523.

Réponse:

523₈

Méthode 2 sur 2: Conversions rapides et variantes

Image intitulée Convertir le nombre binaire en nombre octal, étape 9

1. Utilisez une table de conversion simple pour gagner du temps et du travail. Vous ne pouvez pas l`utiliser sur un test, mais à d`autres moments, c`est un excellent choix. Puisqu`il n`y a que 8 combinaisons de nombres possibles, c`est en fait un tableau assez facile à retenir. Tout ce que vous avez à faire est de diviser les nombres en groupes de trois et de les comparer avec le tableau des images.

Notez comment pour les nombres 8 et 9 il n`y a pas de conversions directes. En nombres octaux n`existent-ils pas puisqu`il n`y a que 8 chiffres (0-7) dans un système de numérotation en base 8.

Image intitulée Convertir le nombre binaire en nombre octal, étape 10

2. Laissez la virgule décimale et déterminez si vous avez affaire à des décimales. Supposons que vous deviez convertir le nombre binaire 10010.11 en nombre octal. Normalement, vous travaillez de droite à gauche pour diviser les nombres en groupes de trois. Avec une décimale, vous travaillez vers l`extérieur à partir du point. Donc pour les chiffres à gauche de la virgule (10010), travaillez du point à gauche (010 010 ou converti, 115,24). Pour les nombres de droite (0,11), travaillez du point vers la droite (110). Lorsque vous ajoutez des zéros, ajoutez-les toujours dans la direction dans laquelle vous travaillez. La distribution finale est 010 010 , 110.

101.1 → 101 . 100

1.01001 → 001 . 010 010

1001101.0101 → 001 001 101 . 010 100

Image intitulée Convertir le nombre binaire en nombre octal, étape 11

3. Utilisez la table de conversion octale pour reconvertir d`octal en binaire. Vous avez besoin de la table pour travailler à l`envers, car un simple "3" ne vous donne pas assez d`informations pour effectuer le calcul à moins que vous ne connaissiez bien le système octal et que vous vouliez considérer chaque combinaison. Utilisez simplement le tableau suivant pour convertir facilement un chiffre octal en une séquence de trois nombres binaires, puis placez-les côte à côte :

0 → 000

1 → 001

2 → 010

3 → 011

4 → 100

5 → 101

6 → 110

7 → 111