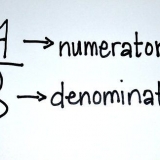
/12 x 180/π = 180π/12π ÷ 12π/12π = 15° /12 radians = 15° 
Exemple 1: 1/3π radians = π/3 x 180/π = 180π/3π ÷ 3π/3π = 60° Exemple 2: 7/4π radians = 7π/4 x 180/π = 1260π/4π ÷ 4π/4π = 315° Exemple 3: 1/2π radians = /2 x 180/π = 180π /2π ÷ 2π/2π = 90° 
Convertir des radians en degrés
Teneur
Les radians et les degrés sont les deux unités de mesure des angles. Comme vous le savez peut-être, un cercle peut être divisé en 2π radians, l`équivalent de 360° ; les deux valeurs représentent une "révolution" d`un cercle. Par conséquent, 1π radians équivaut à 180° degrés dans un cercle, faisant de 180/π l`outil de conversion parfait pour convertir les radians en degrés. Pour convertir un nombre de radians en degrés, il suffit de multiplier la valeur du radian par 180/π. Pour apprendre comment faire cela et comprendre le concept de cette procédure, lisez l`étape 1 pour commencer.
Pas

1. Sachez que π radians est égal à 180 degrés. Avant de commencer la conversion, vous devez savoir que radians = 180°, et que cela équivaut à un demi-cercle. Ceci est important car vous utiliserez 180/π comme unité de conversion. C`est parce que 1π radians est égal à 180/π degrés.

2. Multipliez les radians par 180/π pour convertir en degrés. C`est si simple. Supposons que vous travaillez avec π/12 radians. Ensuite, vous devez multiplier cela par 180/π et simplifier si nécessaire. Cela se passe comme ceci :

3. Entraînez-vous avec quelques exemples. Si vous voulez vraiment vous y habituer, essayez de convertir les radians en degrés avec quelques exemples supplémentaires. Voici quelques autres exercices à revoir :

4. N`oubliez pas qu`il y a une différence entre « radians » et « π radians ». Quand on parle de 2π radians ou 2 radians, ce sont deux termes différents. Comme vous le savez bien, 2π radians équivaut à 360 degrés, mais si vous avez affaire à 2 radians, alors si vous voulez convertir cela en degrés, vous devrez calculer 2 x 180/π. Vous obtenez alors 360/π, soit 114,5°. Ceci est une réponse différente, car si vous ne travaillez pas avec π radians, le ne peut pas être barré dans l`équation, ce qui entraîne une valeur différente.
Des astuces
- Lors de la multiplication, laissez le pi dans vos radians comme symbole, et non l`approximation décimale, afin de pouvoir l`annuler plus facilement lors d`un calcul.
- De nombreuses calculatrices graphiques ont des fonctions de conversion d`unités ou vous pouvez télécharger des programmes qui le font. Demandez à votre professeur de mathématiques si votre calculatrice a une telle fonctionnalité.
Nécessités
- Stylo ou crayon
- Papier
- Calculatrice
Articles sur le sujet "Convertir des radians en degrés"
Оцените, пожалуйста статью
Populaire