Calcul des forces en physique : 8 étapes (avec des images)

Teneur

Pas
- Méthode 1 sur 2: Détermination de la tension sur une seule corde
- Méthode 2 sur 2: Calcul de la tension sur plusieurs cordes

En physique, la tension est la force exercée par une corde, une ficelle, un câble ou un objet similaire sur un ou plusieurs autres objets. Tout ce qui est tiré est suspendu, soutenu ou attaché à une corde.ré. oscille, est soumis à la force de traction. Comme d`autres forces, la tension peut accélérer ou déformer les objets. Être capable de calculer la tension est une compétence importante pour les étudiants en physique, mais aussi pour les ingénieurs et les architectes. Après tout, pour concevoir des bâtiments sûrs, ils doivent savoir exactement si la tension d`un câble peut supporter la charge d`un objet. Continuez à lire à l`étape 1 pour apprendre à calculer le stress dans divers systèmes physiques.

Pas

Méthode 1 sur 2: Détermination de la tension sur une seule corde

Image intitulée Calculer la tension en physique Étape 1

1. Déterminer les forces de chaque côté du fil. La tension dans un brin donné d`une corde est la somme de toutes les forces tirant la corde des deux extrémités. Ne pas oublier: force = masse × accélération. Supposons que la corde soit tendue fortement, alors tout changement dans l`accélération ou la masse des objets que la corde supporte entraînera un changement dans la tension de la corde. Oubliez la constante accélération due à la pesanteur ni l`un ni l`autre - même lorsqu`un système est au repos, chaque composant est exposé à la gravité. La tension dans une corde particulière peut être exprimée comme T = (m × g) + (m × a), où "g" l`accélération est due à la gravité de tout objet supporté par la corde, et "une" est toute autre accélération sur tout objet supporté par la corde.

Par souci de simplicité, nous pouvons supposer que nous avons affaire à unfil idéal – autrement dit, que la corde, le câble, etc. est mince et sans masse, et ne peut pas s`étirer ou se casser.
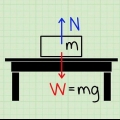
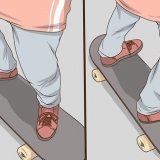
Un exemple : supposons que nous ayons un système où une masse est suspendue à une poutre en bois, attachée avec une seule corde (voir photo). Pourtant, les masses déplacent toujours la corde - tout le système est au repos. Nous savons maintenant que la masse est en équilibre, où la force de tension est égale à la force gravitationnelle sur la masse. En d`autres termes, la tension (F_t) = Force ou Gravité (F_g) = m × g.

Supposons que nous ayons une masse de 10 kg, alors ce qui suit est vrai : tension = 10 kg × 9,8 m/s = 98 Newtons.

Image intitulée Calculer la tension dans l`étape 2 de la physique

2. Attention à l`accélération. La gravité n`est pas la seule force qui affecte la tension d`une corde - toute force peut être associée à l`accélération d`un objet auquel la corde est connectée. Si un objet suspendu est accéléré par une force sur la corde ou le câble, alors la force causée par l`accélération (masse × accélération) est ajoutée à la tension causée par la masse de l`objet.

Supposons dans notre exemple, que la masse de 10 kg soit suspendue à une corde, qui n`est pas attachée à une poutre, mais est utilisée pour soulever la masse avec une accélération de 1 m/s. Dans des cas comme celui-ci, nous devons prendre en compte non seulement l`accélération sur la masse, mais aussi la force gravitationnelle, en résolvant cela comme suit :

F_t = F_g + m × un

F_t = 98 + 10 kg × 1 m/s

F_t = 108 Newtons.

Image intitulée Calculer la tension en physique, étape 3

3. Tenir également compte d`un engrenage circulaire. Un objet qui tourne autour d`un point central sur une corde (comme un pendule) exerce une tension sur la corde causée par la force centripète. La force centripète est la force que la corde exerce sur un objet en le tirant vers l`intérieur "tirer", pour que l`objet continue à se déplacer en arc de cercle, au lieu d`aller tout droit. Plus l`objet se déplace rapidement, plus la force centripète est grande. force centripète (F_c) est égal à m × v/r où "m" est égal à la masse, "v" est la vitesse et "r" est le rayon du cercle, c`est-à-dire la trajectoire sur laquelle l`objet se déplace.

Étant donné que la direction et l`amplitude de la force centripète changent à mesure que l`objet sur la corde se déplace et que la vitesse change, la tension totale de la corde change également, qui tire toujours parallèlement à la corde vers le point central. Rappelez-vous que la constante gravitationnelle tire sur l`objet. Ainsi, si un objet est projeté en position verticale, alors la tension totale est la le plus grand au bas de la trajectoire de l`objet (dans le cas d`une horloge à pendule, on l`appelle aussi l`équilibre), là où l`objet se déplace le plus rapidement. La tension est au moins au sommet du mouvement circulaire, où la vitesse est la plus faible.

Supposons dans l`exemple que l`objet oscille comme un pendule. La corde mesure 1,5 mètre de long et la masse se déplace à une vitesse de 2 m/s au point le plus bas. Si l`on veut calculer la tension en ce point, le point auquel la vitesse est la plus élevée, il faut d`abord voir que la tension due à la gravité en ce point est la même que lorsque le pendule est au repos - 98 Newtons. Pour trouver la force centripète, on calcule comme suit :

F_c = m × f/r

F_c = 10 × 2/1.5

F_c =10 × 2,67 = 26,7 Newtons.

Ainsi, la tension totale est de 98 + 26,7 = 124,7 Newtons.

Image intitulée Calculer la tension en physique, étape 4

4. Comprendre que la tension due à la gravité change pendant la période du pendule. Comme mentionné précédemment, la direction et l`amplitude de la force centripète changent lorsqu`un objet se balance. Mais bien que la gravité reste constante, la tension due à la gravité changer aussi. Comme un objet qui se balance ne pas bas de l`oscillation du pendule (le point d`équilibre), puis la gravité tire vers le bas, mais la tension tire sur l`objet à un angle. Pour cette raison, la tension annulera une partie de la force gravitationnelle, mais pas complètement.

Diviser la gravité en deux vecteurs peut vous aider à mieux visualiser ce concept. À n`importe quel point de l`arc de mouvement d`un objet oscillant, la corde forme un angle de "??" avec la droite passant par l`équilibre et le point central de la rotation. Lorsque la corde oscille, vous pouvez diviser la force de gravité (m × g) en 2 vecteurs - mgsin(θ) est la tangente à l`arc dans la direction de l`équilibre, et mgcos(θ), le parallèle à la force de tension dans le direction opposée. La tension n`a besoin que de s`opposer à mgcos(θ) - la force qui s`oppose - et non à la pleine force de gravité (sauf au point d`équilibre, lorsqu`elle est égale à la tension).

Supposons que le pendule forme un angle de 15 degrés avec la verticale, puis a une vitesse de 1,5 m/s. On trouve la tension comme suit :

Contrainte due à la gravité (T_g) = 98cos(15) = 98(0,96) = 94,08 Newtons

force centripète (F_c) = 10 × 1,5/1,5 = 10 × 1,5 = 15 Newtons

Tension totale = T_g + F_c = 94,08 + 15 = 109,08 Newtons.

Image intitulée Calculer la tension en physique, étape 5

5. Pensez aussi au frottement. Tout objet tiré à travers une corde et subissant la friction d`un autre objet (ou liquide) transfère cette force de friction à la tension de la corde. La force de frottement entre deux objets est calculée de la même manière que dans toute autre situation - par l`équation suivante : Force par frottement F_r = (mu)N, où mu est le coefficient de frottement entre les deux objets et où N est la force normale entre les deux objets (la force avec laquelle ils se pressent l`un contre l`autre). Notez que la friction statique – la friction qui se produit lorsque vous essayez de déplacer un objet immobile – est différente de la friction cinétique – la friction qui se produit lorsque vous essayez de maintenir un objet en mouvement en mouvement.

Supposons que la masse de 10 kg ne se balance plus, mais qu`elle soit traînée horizontalement sur le sol et sur une corde. On dit maintenant que le sol a un coefficient de frottement cinétique de 0,5 et que la masse se déplace à vitesse constante, mais on veut l`accélérer à 1 m/s. Cette nouvelle affectation révèle deux changements importants - le premier est que nous n`avons plus besoin de calculer la tension due à la gravité, car la corde ne supporte plus la masse et contrecarre la force. Nous devons maintenant prendre en compte la force de frottement et la contrainte résultante, ainsi que la contrainte causée par l`accélération de l`objet. Nous résolvons cela comme suit :

Force normale (N) = 10 kg × 9.8 (accélération par gravité) = 98 N

Force de frottement cinétique (F_r) = 0.5 × 98 N = 49 Newtons

Force d`accélération (F_une) = 10 kg × 1 m/s = 10 Newton

Tension totale = F_r + F_une = 49 + 10 = 59 Newtons.

Méthode 2 sur 2: Calcul de la tension sur plusieurs cordes

Image intitulée Calculer la tension en physique, étape 6

1. Levage de charges verticales parallèles avec une poulie. Une poulie est une machine simple constituée d`une roue suspendue qui permet à la force de tension d`une corde de changer de direction. Dans une configuration simple, la corde ou le câble passe d`une masse suspendue à travers la poulie, puis descend à une autre masse, vous donnant deux longueurs de corde. Mais la tension dans les deux parties de la corde est la même, même si des masses de tailles différentes pendent des deux extrémités de la corde. Dans un système de deux masses suspendues à une poulie, la tension est égale à 2g(m₁)(m₂)/(m₂+m₁), par lequel "g" l`accélération est due à la gravité, "m₁" la masse de l`objet 1 et "m₂" la masse de l`objet 2.

Notez que nous supposons un "poulie idéale – pas de masse, pas de friction et des poulies qui ne peuvent se casser, se déformer ou se détacher du plafond.
Supposons que nous ayons deux masses suspendues à une poulie, sur des cordes parallèles. Le poids 1 a une masse de 10 kg et le poids 2 a une masse de 5 kg. Dans ce cas, nous trouvons la tension comme suit:

T = 2g(m₁)(m₂)/(m₂+m₁)
T = 2(9.8)(10)(5)/(5 + 10)
T = 19,6(50)/(15)
T = 980/15
T = 65,33 newtons.

Notez que parce qu`une masse est plus lourde que l`autre, le système accélérera, les 10 kg descendant et les 5 kg montant.

2. Soulever des poids avec une poulie sur des cordes verticales mais non parallèles. Les poulies sont souvent utilisées pour obtenir une tension dans une direction autre que vers le haut ou vers le bas. Par exemple, si une masse pend verticalement à une extrémité de la corde, tandis qu`une deuxième masse est attachée sur une pente à l`autre extrémité, ce système de poulies non parallèles prendra la forme d`un triangle dont les sommets sont la première masse, la deuxième masse et la poulie elle-même. Dans ce cas, la tension dans la corde est déterminée à la fois par la gravité sur la masse et par la composante de la force de traction agissant parallèlement à la portion diagonale de la corde.

Supposons que nous ayons un système avec une masse de 10 kg (m₁), relié verticalement, par l`intermédiaire d`une poulie, d`une masse de 5 kg (m₂) sur une pente de 60 degrés (nous supposons que la pente est sans friction). Pour trouver la tension dans la corde, il est plus facile d`être le premier à formuler des équations pour les forces accélérant les masses. Procédez comme suit:

La masse suspendue est plus lourde et nous n`avons pas à tenir compte du frottement, nous savons donc qu`il y a une accélération vers le bas. Mais la tension dans la corde tire la masse vers le haut, nous calculons donc la force nette sur la corde comme suit : F = m₁(g) - T, ou 10(9.8) - T = 98 - T.

On sait que la masse va accélérer sur la pente. Puisque la pente est sans friction, nous savons que la tension tire la masse vers le haut de la pente, retenue uniquement par la propre masse du poids. La composante de force qui tire le poids vers le bas est calculée par mgsin(θ), donc dans notre cas, nous pouvons dire que le poids en montée accélère la pente par la force nette F = T - m₂(g) sin(60) = T - 5(9.8)(.87) = T - 42.63.

L`accélération des deux masses est la même, on a donc (98 - T)/m₁ = T - 42.63 /m₂. Après quelques algèbres simples, nous obtenons T = 61.09 Newton.

Image intitulée Calculer la tension en physique, étape 8

3. Utiliser plusieurs cordes pour accrocher un objet. Enfin, nous considérons le cas où un objet est suspendu à un "en forme de Y" système de cordes - deux cordes sont fixées au plafond et se rejoignent en un point central, où un poids est suspendu à une troisième corde. La tension dans la troisième corde est évidente - c`est simplement la tension résultante due à la gravité. Les tensions dans les deux autres cordes sont différentes et lorsqu`elles sont additionnées, elles doivent être égales à la gravité dans le sens ascendant et vertical, et égales à zéro dans le sens horizontal (en supposant que le système est au repos). La tension dans les cordes est affectée par la masse de l`objet suspendu ainsi que l`angle de chaque corde par rapport au plafond.

Supposons dans ce système en forme de Y, que l`objet pèse 10 kg et que les deux cordes supérieures forment un angle avec le plafond de 30 degrés et 60 degrés. Si nous voulons trouver la tension dans chacune des cordes supérieures, nous devons considérer les composantes verticales et horizontales de la tension pour chaque corde. Les deux cordes de cet exemple pendent perpendiculairement l`une à l`autre, ce qui facilite le calcul de ces contraintes, selon les définitions des fonctions trigonométriques. Donc comme suit :

Le rapport entre T₁ ou T₂ et T = m(g) est égal au sinus de l`angle entre chaque câble porteur et le plafond. pour T₁ est sin(30) = 0,5, tandis que pour T₂ soutient que sin(60) = 0,87.

Multipliez la tension dans la corde inférieure (T = mg) par le sinus de chaque angle, pour obtenir T₁ et T₂ trouver.

t₁ =0,5 × m(g) =0,5 × 10(9,8) = 49 Newtons.

t₂ =0,87 × m(g) =0,87 × 10(9,8) = 85,26 newtons.