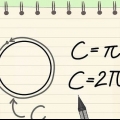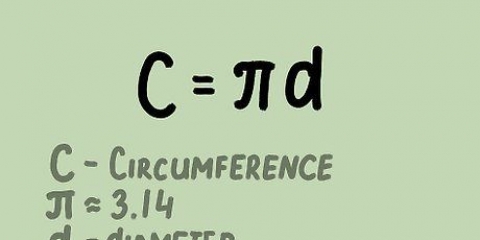Mémoriser le cercle d'unité : 14 étapes (avec des images)

Teneur

Pas
- Partie 1 sur 2: Rappelez-vous les radians
- Partie 2 sur 2: Rappelez-vous les coordonnées x et y (cosinus, sinus)
Des astuces

Apprendre le cercle unité vous aidera non seulement avec la trigonométrie et la géométrie, mais aussi avec le calcul différentiel et intégral. Cela peut sembler beaucoup de mémorisation, mais une fois que vous avez compris comment cela fonctionne, vous pouvez commencer avec quelques chiffres du cercle unité et comprendre rapidement le reste.

Pas

Partie 1 sur 2: Rappelez-vous les radians

Image intitulée Mémorisez le cercle de l`unité Étape 1

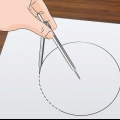
1. Tracez deux lignes perpendiculaires. Placer une boussole sur une grande feuille de papier. Tracez une ligne verticale et une ligne horizontale. Ceux-ci doivent se croiser près du centre de la page. Ce sont l`axe des x et l`axe des y du graphique.

Image intitulée Mémorisez le cercle de l`unité Étape 2

2. Dessiner un cercle. À l`aide d`une boussole, tracez un grand cercle centré à l`intersection des deux lignes.

Image intitulée Mémorisez le cercle de l`unité Étape 3

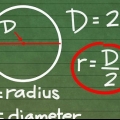
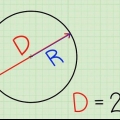
3. Comprendre les radians. Un radian est une mesure d`angle. Il est principalement défini de telle manière qu`une personne marchant autour d`un cercle avec un Rayon de 1 unité se déplace sur un angle d`un radian après avoir parcouru 1 unité autour du périmètre. Dans l`étape suivante, nous indiquerons les quatre points de coordonnées avec la valeur en radian. Si vous vous souvenez de la formule de la relation entre la circonférence d`un cercle et son rayon, vous pouvez la calculer rapidement, mais même si vous ne vous en souvenez pas.

Les mesures en radian du cercle unité supposent toujours que vous partez du point (0, 1). Pour préciser à quel point nous nous référons, nous décrivons le cercle comme une rose des vents :

Image intitulée Mémorisez le cercle de l`unité Étape 4

4. Rappelez-vous que la circonférence du cercle est de 2π. La circonférence d`un cercle est égale à 2πr, par lequel r représente le rayon (le rayon). Puisque le cercle unité a un rayon de 1, nous pouvons simplifier la circonférence à 2π. La valeur en radian de n`importe quel point de la circonférence peut être trouvée en divisant simplement 2π par la partie du cercle que vous aviez. C`est beaucoup plus facile que de mémoriser chaque valeur sur le cercle.

Image intitulée Mémorisez le cercle de l`unité Étape 5

5. Indiquer les quatre points sur les axes x et y. Tout ce que vous avez à faire est de diviser 2π en quarts :

« Est » est le point de départ, vous avez donc 0 avait des radians.

`Nord` = un quart de la circonférence du cercle = /₄ = /₂ radians.

`Ouest` = à mi-chemin du cercle = /₂ = ?? radians.

`Sud` = trois quarts du cercle = 2π * ¾ = /₂ radians.

Si vous parcourez tout le périmètre, vous revenez au point de départ. Vous pouvez l`indiquer comme 2π ou 0.

Image intitulée Mémorisez le cercle de l`unité Étape 6

6. Divisez le cercle en huit morceaux. Tracez maintenant une ligne diagonale à travers chaque quadrant, parfaitement à travers le centre. Encore une fois, utilisez la division pour trouver la valeur en radians :

/₄

(π/2, π, 3π/2 et 2π ont déjà été indiqués.)

Image intitulée Mémorisez le cercle de l`unité Étape 7

sept. Divisez le cercle en six segments. Tracez maintenant des lignes supplémentaires qui divisent le cercle en six segments. (Vous pouvez utiliser un rapporteur pour cela, en commençant par l`axe x positif, où chaque segment mesure 60 degrés). Vous pouvez utiliser la même approche que ci-dessus pour vous assurer qu`un sixième de cercle est égal à /₆ = /₃ radians. Utilisez cette étiquette pour les points suivants du périmètre (un dans chaque quadrant) :

/₃

(π et 2π sont déjà indiqués)

Image intitulée Mémorisez le cercle de l`unité Étape 8

8. Dessine-y les douzièmes. Les derniers points marqués sur la plupart des cercles unitaires indiquent des incréments d`un douzième de la circonférence. Seuls quatre d`entre eux n`ont pas encore été déclarés :

/₆

Partie 2 sur 2: Rappelez-vous les coordonnées x et y (cosinus, sinus)

Image intitulée Mémorisez le cercle de l`unité Étape 9

1. Comprendre le cosinus et le sinus. Le cercle unité est particulièrement utile pour les calculs trigonométriques avec des angles droits. Toute coordonnée x d`un point sur le cercle est égale à cos(θ) et toute coordonnée y est égale à sin(θ), où est la valeur de l`angle.

Si vous avez du mal à vous en souvenir, pensez à (cos, sin) `parce que le sinus vient en dernier`.
Vous pouvez le déduire en utilisant des triangles rectangles et la définition de ces fonctions — rappelez-vous « soscastoa »?

Image intitulée Mémorisez le cercle de l`unité Étape 10

2. Notez les coordonnées en quatre points du cercle. Un « cercle unitaire » est simplement un cercle avec un rayon d`exactement une unité. Utilisez-les pour trouver les coordonnées x et y des quatre points du cercle où il coupe un axe. (Nous les appelons « Est », « Nord », etc. pour faciliter la lecture, mais ce ne sont pas des noms officiels).

Les coordonnées de « Est » sont (dix).

Les coordonnées du `Nord` sont (0, 1).

Les coordonnées de « Ouest » sont (-dix).

Les coordonnées du `Sud` sont (0, -1).

Cela fonctionne comme un graphique normal. Vous devriez pouvoir trouver ces coordonnées vous-même, sans avoir à les mémoriser.

Image intitulée Mémorisez le cercle de l`unité Étape 11

3. Mémoriser les coordonnées du premier quadrant. Le premier quadrant est le quart supérieur droit du cercle, où les deux valeurs x comme le oui-les valeurs sont positives. Ce sont les seules coordonnées dont vous devez vous souvenir :

Au /₆, sont les coordonnées ( $\frac{\sqrt{3}}{2}, \frac{1}{2}$ ${frac{{sqrt{3}}}{2}},{frac{1}{2}}$ ).

Au /₄, sont les coordonnées ( $\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}$ ${frac{{sqrt{2}}}{2}},{frac{{sqrt{2}}}{2}}$ ).

Au /₃, sont les coordonnées ( $\frac{1}{2}, \frac{\sqrt{3}}{2}$ ${frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ).

Notez qu`il n`y a que trois compteurs. Allez-vous dans une direction positive (de gauche à droite pour le valeurs x, de bas en haut pour le valeurs y), alors la suite est la suivante : 1 → √2 → √3.

Image intitulée Mémorisez le cercle de l`unité Étape 12

4. Tracez des lignes droites pour remplir les autres coordonnées. Si vous pouvez tracer une ligne parfaitement verticale ou parfaitement horizontale entre deux points, alors ils ont la même valeur absolue que les coordonnées x et y. En d`autres termes, vous pouvez tracer une ligne à partir d`un point dans les premiers quadrants, écrire les mêmes coordonnées au point où vous atterrissez et laisser un espace à sa droite pour le signe (+ ou -).

Par exemple, vous pouvez tracer une ligne horizontale entre /₃ et /₃. Puisque les coordonnées du premier point (

\frac{1}{2}, \frac{\sqrt{3}}{2}

${frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ), les coordonnées du deuxième point (?

\frac{1}{2}, ? \frac{\sqrt{3}}{2}

${frac{1}{2}}, ?{frac{{sqrt{3}}}{2}}$ ), par lequel `?` représente un signe plus ou moins (+ ou -).

Voici un moyen plus rapide : vérifiez le dénominateur des radians. Tous les points se terminant par /3 ont les mêmes coordonnées absolues, tout comme tous les points se terminant par /4 et tous les points se terminant par /6.

Image intitulée Mémorisez le cercle de l`unité Étape 13

5. Utilisez la symétrie pour savoir si le signe est positif ou négatif. Il existe plusieurs façons de se rappeler où placer les signes moins sur le cercle de l`unité :

Pensez aux règles fondamentales des graphiques. Au dessus de X-axe les points sont positifs, en dessous négatifs. A gauche du oui est négatif, la droite est positive.

Commencez à partir du quadrant 1 et tracez des lignes vers d`autres points. Si la ligne de oui-l`axe croise la valeur y changera de signe. Si la ligne de X-l`axe se croise, puis la valeur x change de signe.

Apprenez « Tous les élèves testent le calcul » (ASTC), dans le sens inverse des aiguilles d`une montre. Le quadrant 1 a uneuniquement des valeurs positives, le quadrant 2 n`a que des valeurs positives svaleurs inus, le quadrant 3 n`a que des valeurs positives tvaleurs d`angens, et le quadrant 4 n`a que des valeurs positives Cvaleurs d`osine.

Quelle que soit la méthode choisie, les signes sont (+, +) pour le quadrant 1, (-, +) pour le quadrant 2, (-, -) pour le quadrant 3 et (+,-) pour le quadrant 4.

Image intitulée Mémorisez le cercle de l`unité Étape 14

6. Vérifie ton travail. Voici la liste complète des valeurs de coordonnées pour chaque point étiqueté sur le cercle (sans compter les quatre points sur les axes), dans le sens des aiguilles d`une montre. N`oubliez pas que vous devriez pouvoir trouver toutes ces valeurs simplement en mémorisant les points du quadrant 1 :

Quadrant 1 : (

\frac{\sqrt{3}}{2}, \frac{1}{2}

${frac{{sqrt{3}}}{2}},{frac{1}{2}}$ ); (

\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}

${frac{{sqrt{2}}}{2}},{frac{{sqrt{2}}}{2}}$ ); (

\frac{1}{2}, \frac{\sqrt{3}}{2}

${frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ).

Quadrant 2 : (

- \frac{1}{2}, \frac{\sqrt{3}}{2}

$-{frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ); (

- \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}

$-{frac{{sqrt{2}}}{2}},{frac{{sqrt{2}}}{2}}$ ); (

- \frac{\sqrt{3}}{2}, \frac{1}{2}

$-{frac{{sqrt{3}}}{2}},{frac{1}{2}}$ )

Quadrant 3 : (

- \frac{\sqrt{3}}{2}, - \frac{1}{2}

$-{frac{{sqrt{3}}}{2}},-{frac{1}{2}}$ ); (

- \frac{\sqrt{2}}{2}, - \frac{\sqrt{2}}{2}

$-{frac{{sqrt{2}}}{2}},-{frac{{sqrt{2}}}{2}}$ ); (

- \frac{1}{2}, - \frac{\sqrt{3}}{2}

$-{frac{1}{2}},-{frac{{sqrt{3}}}{2}}$ )

Quadrant 4: (

\frac{1}{2}, - \frac{\sqrt{3}}{2}

${frac{1}{2}},-{frac{{sqrt{3}}}{2}}$ ); (

\frac{\sqrt{2}}{2}, - \frac{\sqrt{2}}{2}

${frac{{sqrt{2}}}{2}},-{frac{{sqrt{2}}}{2}}$ ); (

\frac{\sqrt{3}}{2}, - \frac{1}{2}

${frac{{sqrt{3}}}{2}},-{frac{1}{2}}$ )

Des astuces

Si vous avez un test ou une répétition sur le cercle de l`unité, dessinez d`abord le cercle sur du papier brouillon afin de pouvoir l`utiliser comme référence pour chaque problème.
Le processus sera considérablement plus rapide si vous pratiquez beaucoup. À l`avenir, vous n`aurez peut-être besoin que de voir les axes x et y pour vous souvenir de tout, ou vous n`aurez peut-être même plus besoin d`un graphique.